Rédaction - dérivée
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Blup
- Membre Naturel
- Messages: 15
- Enregistré le: 29 Juil 2010, 13:56
-
 par Blup » 29 Juil 2010, 14:08
par Blup » 29 Juil 2010, 14:08
Bonjour, j'ai besoin d'un coup de main pour la justification du signe de f'(x).
Voila la fonction de base, définie sur [0;2pi]
=\frac{cos(x)}{1-sin(x)})
Dérivée:
=\frac{1}{1-sin(x)}) Justification du signe de la dérivée:
Justification du signe de la dérivée:)
est du signe de
})
or
 )>0)
pour tout x appartenant à Df. Donc f'(x)>0 pour tout x appartenant à Df.
Voila, je ne sais pas si la justification est complète et si elle est correctement rédigée. Merci d'avance pour votre aide. :++:
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 29 Juil 2010, 15:41
par Finrod » 29 Juil 2010, 15:41
Tu ne connais aucun angle pour lequel le sinus vaut 1 ?
-
Blup
- Membre Naturel
- Messages: 15
- Enregistré le: 29 Juil 2010, 13:56
-
 par Blup » 29 Juil 2010, 15:46
par Blup » 29 Juil 2010, 15:46
Le sinus vaut 1 pour un angle de pi /2. Quelle serait pour toi la justification la plus correcte pour le signe de f'(x). Je me suis légèrement embrouillé.
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 29 Juil 2010, 15:55
par Finrod » 29 Juil 2010, 15:55
La justification est correcte, c'est l'intervalle de définition qui est faux.
Regarde ce que vaut ta fonction pour x=pi/2
-
Blup
- Membre Naturel
- Messages: 15
- Enregistré le: 29 Juil 2010, 13:56
-
 par Blup » 29 Juil 2010, 15:58
par Blup » 29 Juil 2010, 15:58
Df =

\

? ( avec k , entier relatif )
En fait, c'est l'énoncé qui stipule "
=\frac{cos(x)}{1-sin(x)})
sur [0,2pi]".
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 29 Juil 2010, 16:03
par Finrod » 29 Juil 2010, 16:03
Blup a écrit:Voila la fonction de base, définie sur [0;2pi]
donc seul
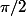
pose pb.
-
Blup
- Membre Naturel
- Messages: 15
- Enregistré le: 29 Juil 2010, 13:56
-
 par Blup » 29 Juil 2010, 16:11
par Blup » 29 Juil 2010, 16:11
Donc, le deuxième Df est correct et la justification pour le signe de f ' ( x) aussi ?
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 29 Juil 2010, 17:16
par Finrod » 29 Juil 2010, 17:16

et le sinus est bien strictement plus petit que 1 sur cet intervalle. (chose fausse en
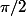
)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 129 invités