Bonjour je cherche a repondre à un problème de maths assez compliquer pour ma part je ne vois pas du tout comment résoudre ^^
" pour tout n IN on pose Un = Somme ( de K= 0 à n ) k²
il fallait calculer U0 , U1 , U2 et U3 ( ça j'ai réussi , c'est simple vous me direz ^^ )
Ensuite Il s'agit d'un système de trois équations à trois incconues
a+b+c=1
8a+4b+2c=5
27a+9b+3c=14
et pour terminer il faut montrer par recurrence sur nIN que :
Un = ( 2n^3+3n²+n)/6
Je vous remercie d'avance d'avoir lu cet exercice et aussi d'y repondre si vous voyez comment faire pour les deux dernières questions ^^
DM maths Term S
3 messages
- Page 1 sur 1
Bonsoir,
pour le système à trois équations et trois inconnues,
tu sais le résoudre si tu sais résoudre un système de deux équations à 2 inconnues : la première équation se réécrit c=1-a-b, et tu remplaces c par 1-a-b dans les deux autres équations ; après avoir un peu développé et réduit, tu te ramènes à un système de niveau collège...
Bon en même temps en TS tu dois connaître le pivot de Gauss (sinon demande à un TES spé math).
Pour la récurrence, bah tu commences par vérifier que ton polynome donne bien la somme des carrés des n premiers entiers pour n = 1 !
Ensuite il suffit de prouver que P(n+1)=P(n) + (n+1)².
Le plus simple est de partir de P(n+1)-P(n)-(n+1)², de développer et de réduire, pour trouver zéro.
P est bien sûr le polynôme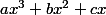 avec les a, b et c que tu as trouvé en résolvant le système.
avec les a, b et c que tu as trouvé en résolvant le système.
pour le système à trois équations et trois inconnues,
tu sais le résoudre si tu sais résoudre un système de deux équations à 2 inconnues : la première équation se réécrit c=1-a-b, et tu remplaces c par 1-a-b dans les deux autres équations ; après avoir un peu développé et réduit, tu te ramènes à un système de niveau collège...
Bon en même temps en TS tu dois connaître le pivot de Gauss (sinon demande à un TES spé math).
Pour la récurrence, bah tu commences par vérifier que ton polynome donne bien la somme des carrés des n premiers entiers pour n = 1 !
Ensuite il suffit de prouver que P(n+1)=P(n) + (n+1)².
Le plus simple est de partir de P(n+1)-P(n)-(n+1)², de développer et de réduire, pour trouver zéro.
P est bien sûr le polynôme
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
