Exos produit scalaire

[vaval59]

bonjour a tous , voila 2 exercices que je n arrive pas du tout a faire ... j avais quelques pistes mais celles ci aboutissent a un mauvais résultat ...

1er exo :
dans un triangle ABC , I est le milieu de [AB]. démontrer les relations suivantes :
1) AC²+BC²= 2 CI²+1/2AB²
2) AC²-BC²= 2 ( vecteurs CI.BA)
3) BC²=AB²+AC²-2AB*AC*cos( angle BAC)


le deuxieme exercice etant aussi sur le produit scalaire dans l espace :

l'espace est muni d un repere orthonormal.
soit (d) la droite passant par A(2;0;1) et de vecteur directeur u (1;1;1) et soit le point B (3;2;4).
determiner les coordonnées du projeté orthogonal de B sur (d)



voila voila .. mercid avance pour votre aide ^^'

[Ericovitchi]

Pour 1) AC²+BC²= 2 CI²+1/2AB²
tu pars de AC²+BC² et tu remplaces AC=AI+IC (en vecteurs) et BC=BI+IC
tu développes les carrés et tu utilises le fait que IA+IB=0 pour simplifier et tomber sur l'expression de droite.

Pour 2) AC²-BC² tu utilises a²-b²=(a+b)(a-b) (en vecteurs !) et tu trouves très vite

Pour le 3) tu écris BC=BA+AC (en vecteur) et tu élèves au carré

[vaval59]

ok ok merci bien .. et pour l autre exercice tu as une idée ??
moi j ai trouvé une equation d un plan .. mais apres je sais pas vers quoi partir pour trouver les coordonnées du projeté ...

[Ericovitchi]

Tous les points de la droite (d) sont tels que
(avec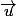 (1,1,1) le vecteur directeur)

donc les points de la droite (d) ont pour coordonnées
(ce sont les coordonnées paramétriques de la droite on appelle ça)
x=2+k
y=k
z=1+k

Donc un vecteur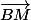 a pour coordonnées ?
Il ne te suiffit plus qu'à écrire que le point que tu cherches est tel que BM est perpendiculaire au vecteur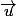 ou encore que
ça te fait une équation à un inconnue k, tu vas trouver k puis les coordonnées du point M correspondant.