Calcul d'intégrale

[CloudCompany]

Bonjour, je souhaiterai vous soumettre un exercice pour savoir si vous trouvez les même résultat que moi car je ne suis pas sur de la méthode que j'ai employé durant l'exercice.

Alors :

Soit un réel strictement positif.

1°) On pose

a) Exprimer en fonction de
b) Déterminer

2°) On pose

a) En utilisant une intégration par parties, exprimer en fonction de et de , puis en fonction de .

b) Déterminer

[Nightmare]

Salut,

vu que tu doutes de ta méthode, l'idéal serait que tu postes tes réponses avec leur justification non?

[CloudCompany]

Pouvez-vous me dire vos résultats ?

J'ai trouvé pour 1 a) :



Ensuite pour la 1 b) :





Ensuite pour la 2 a)

puis



Ensuite pour la 2 b)

[CloudCompany]

Salut,

vu que tu doutes de ta méthode, l'idéal serait que tu postes tes réponses avec leur justification non?

Il n'y a pas 36 méthodes pour calculer une intégrale.
Pour la 1) a)

J'ai F(1) - F()

Ensuite pour la limite j'ai trouvé que cela faisait - car tend vers 0 quand tend vers 0.

Etes vous d'accord avec cela ?

[Black Jack]

1°)

Poser -1/t = u

dt/t² = du

L'intégrale est donc équivalente à

Et cela c'est immédiat...

:zen:

[Nightmare]

Il n'y a pas 36 méthodes pour calculer une intégrale.
Pour la 1) a)

J'ai F(1) - F()

Ensuite pour la limite j'ai trouvé que cela faisait - car tend vers + quand tend vers 0.

Etes vous d'accord avec cela ?

Ok pour l'intégrale. Concernant la limite, il faut distinguer la limite à gauche ou à droite car -1/alpha tend vers +oo si alpha tend vers 0 par valeur négatives !

[CloudCompany]

1°)

Poser -1/t = u

dt/t² = du

L'intégrale est donc équivalente à

Et cela c'est immédiat...

:zen:

Donc la première question est juste.
Pour la limite vous êtes d'accord avec moi ?

[CloudCompany]

Ok pour l'intégrale. Concernant la limite, il faut distinguer la limite à gauche ou à droite car -1/alpha tend vers +oo si alpha tend vers 0 par valeur négatives !

Pour le coup est un réel STRICTEMENT positif.

[Nightmare]

Ok, je n'avais pas lu cela. Dans ce cas la limite est juste.

[CloudCompany]

Ok, je n'avais pas lu cela. Dans ce cas la limite est juste.

Je viens de m'apercevoir d'un truc que j'avais pas fais gaffe c'est dans le calcul de la limite, c'est c'est pas qui faut montrer, c'est

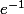
Donc la limite c'est quand tend vers 0

[CloudCompany]

Pour la 2) a), j'ai décomposé l'intégrale en Ca marche ou pas ?