Je pense que c'est le troisième jour. Je serais vraiment heureux d'avoir fini avec ça. J'ai essayé de congruence, Fermat, les qualités de triplets de Pythagore, mais ça va pas. S'il vous plaît aidez-moi.
équation - triples
7 messages
- Page 1 sur 1
équation - triples
Les nombres  sont premiers entre eux. Montrer que l'équation
sont premiers entre eux. Montrer que l'équation 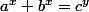 a une infinité de solutions en nombres entiers positifs
a une infinité de solutions en nombres entiers positifs ) .
.
Je pense que c'est le troisième jour. Je serais vraiment heureux d'avoir fini avec ça. J'ai essayé de congruence, Fermat, les qualités de triplets de Pythagore, mais ça va pas. S'il vous plaît aidez-moi.
Je pense que c'est le troisième jour. Je serais vraiment heureux d'avoir fini avec ça. J'ai essayé de congruence, Fermat, les qualités de triplets de Pythagore, mais ça va pas. S'il vous plaît aidez-moi.
Presque...
Il te faut un peut plus "fort" que ça : si tu veut que puisse s'écrire
puisse s'écrire  pour un certain entier c, il faut que xn+1 soit de la forme ky avec k entier (
pour un certain entier c, il faut que xn+1 soit de la forme ky avec k entier (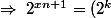^y) ).
).
Il faut donc que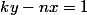 et, comme x et y sont premier entre eux, on sait qu'il existe une infinité de tels n.
et, comme x et y sont premier entre eux, on sait qu'il existe une infinité de tels n.
Il te faut un peut plus "fort" que ça : si tu veut que
Il faut donc que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
