Bonjour, voici le problème sur lequel je me suis cassé les dents tout le week end....
Je me donne une première hyperbole dans le plan

d'équation :

Je ne m'intèresse qu'à la nappe "positive", je peux exprimer
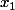
en fonction de
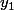
d'après la relation précédente par :
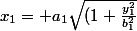})
Je me donne une seconde hyperbole

d'équation :

Ici encore je ne m'intèresse qu'à l'une des deux nappes et ai donc :
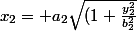})
Je décide ensuite d'orienter l'hyperbole

(respectivement

) d'un angle

(respectivement

)
Je passe donc par les matrices de rotations et expriment

et

sous la forme :


Idem pour la deuxième hyperbole :


J'ai vérifié ces équations sur Matlab en faisant un
)
et
)
, tout marche bien, j'arrive à tracer ces hyperboles orientées.
Mon problème est que je n'arrive pas à déterminer analytiquement le point d'intersection de ces deux hyperboles. C'est assez frustrant car j'ai l'impression d'avoir toutes les équations entre les mains, pourtant tous mes essais se sont soldés par un echec, donc si quelqu'un peut m'éclairer... même pour un cas simple du type

et

ce serait génial !
Merci beaucoup.
