Bonjour pourriez vous m'aider,
1) Démontrer que, a et n étant deux entiers naturels, si a^n-1 est premier alors a est egal à 2 et n premier.
a) pour chacun des nombres suivants dire si se sont des nombres premiers: 2^7-1, 3^7-1, 2^4-1
b) En utlisant une factorisation de a^n-1 demontrer que si a^n-1 est premier alors a est egal à 2
2) Par un raisonnement par l'absurde, si 2^n-1 est premier alors n est premier. Justifier que la reciproque de cette proposition est fausse.
Spé maths
2 messages
- Page 1 sur 1
Bonsoir,
pour le 1a), on a ,
, et
et ; la question (de niveau sixième) est de savoir si chacun de ces nombres est premier ; une petite question facile pour s'échauffer, en fait.
; la question (de niveau sixième) est de savoir si chacun de ces nombres est premier ; une petite question facile pour s'échauffer, en fait.
Pour le 1b), la méthode t'est donnée : utilise l'identité remarquable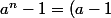(a^{n-1}+a^{n-2}+...+a^2+a+1)) , que tu connais peut-être mieux sous la forme
, que tu connais peut-être mieux sous la forme  pour q différent de 1 ; tu as vu cette formule en 1ère, dans le chapitre sur les suites géométriques.
pour q différent de 1 ; tu as vu cette formule en 1ère, dans le chapitre sur les suites géométriques.
Pour la question 2), commences par énoncer la réciproque demandée, puis prouve que cette réciproque est fausse : pour cela il suffit de chercher un contre exemple, c'est-à-dire un nombre n premier tel que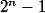 n'est pas premier.
n'est pas premier.
pour le 1a), on a
Pour le 1b), la méthode t'est donnée : utilise l'identité remarquable
Pour la question 2), commences par énoncer la réciproque demandée, puis prouve que cette réciproque est fausse : pour cela il suffit de chercher un contre exemple, c'est-à-dire un nombre n premier tel que
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
