Exercice :
Un producteur de patate peut récolter à ce jour 1 200kg et les vendre 1 le kg. S'il attend, sa récolte augmentera de 60kg par jour, mais le prix baissera de 0.02 par kg, et par jour.
1° Calculer sont chiffre d'affaires dans chaques cas:
a/ s'il vend toute sa récolte tout de suite
b/ s'il attend un mois avand de vendre,
2° On suppose que ce producteur attend "n" jours, "n" entiers de 0 à 50.
a/ exprimer la quantité Q(n) de patates en fonctions du nombre de jour "n".
b/ exprimer le prix de vente P(n) d'un kilogramme de patates en fonction de "n".
c/ en déduire le chiffre d'affaires R(n) de ce producteur.
3° Déterminer le jour "n" où ce producteur aura un chiffre d'affaires maximal
Mon Travail:
1)a) 1200x1 = 1200
1)b) 30x0.02 = 0.6 de baisse, que j'enleve à 1, j'obtien 0.4, prix d'un kilogrames de patates apres 1 mois d'attente. s'il produit 3000kg (1200+30x60), son chiffre d'affaire sera 3000x0.4 = 1200, le C.A n'a pas bouger !
2)a) Q(n) = 1200+60n
2)b) P(n) = 1-0.02n
2)c) R(n) = Q(n) x P(n)
= (1200 x 60n) (1-0.02n)
R(n)= -1.2² +36n +1200
3) Flou total, incompréhension totale
Cordialement
Aide sur Polynome
9 messages
- Page 1 sur 1
Si tu n'as pas vu les dérivées, il faut procéder différement.
Je te propose deux méthodes :
1) Une trés bébète : tu prend un tableur et tu lui demande de calculer les valeurs de -1.2n²+36n+1200 pour tout les entiers n de 0 à 50 puis tu regarde laquelle est la plus grande.
2) En utilisant ce que l'on appelle la "forme canonique" d'un trinôme du second degrés :
\ =\ -1,2(n^2-2\times15n+15^2-15^2-1000))
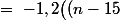^2-1225\big)\ =\ 1470-1,2(n-15)^2\ \leq\ 1470) avec égalité si
avec égalité si 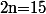
Je te propose deux méthodes :
1) Une trés bébète : tu prend un tableur et tu lui demande de calculer les valeurs de -1.2n²+36n+1200 pour tout les entiers n de 0 à 50 puis tu regarde laquelle est la plus grande.
2) En utilisant ce que l'on appelle la "forme canonique" d'un trinôme du second degrés :
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben... la "forme canonique", c'est exactement ce que j'ai écrit dans le post précédent, cela consiste en une "grosse astuce" consistant à faire apparaitre une identité remarquable à un endroit où il n'y en as pas vraiment une...
Ici, cela consiste à écrire que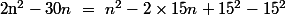 pour "faire apparaitre" une identité remarquable de la forme (a-b)².
pour "faire apparaitre" une identité remarquable de la forme (a-b)².
Si tu n'a pas vu cette "astuce", il me semble que cela signifie qu'il ne te reste que la méthode "tableur"...
Ici, cela consiste à écrire que
Si tu n'a pas vu cette "astuce", il me semble que cela signifie qu'il ne te reste que la méthode "tableur"...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
re
Oui, mais c'est un Dm et il faut argumenté un minimum par un calcul, et je ne serai point faire la méthode du tableur non plus, pourrait tu me donner la réponse s'il te plait ?
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
