Simplification avec ln et exp

par **lycfabert/rom** » 09 Déc 2009, 00:25

salut tout le monde!

voilà, je voudrais simplifier cette expression:
20*A*(1,1)^A=B (où B est donné et A entier)
de manière à avoir une expression de la forme:
A=C (où C est une formule indépendante de A càd dont la valeur ne dépend pas de A).

Mais comment y parvenir? Je pense qu'il faut passer par ln et exp, mais je n'y arrive pas! Je précise que ce n'est pas un exercice, c'est pour le fun donc je ne sais pas si c'est réalisable.

S'il faut le developper de la manière suivante (A=C) c'est parce que cette expression sera utilisé dans excel; pour l'instant, on donne une valeur entière dans la case A et excel nous donne la valeur de B dans une autre case; je voudrais faire l'inverse (donner B pour avoir A) et si on n'isole pas complétement A, on a des calculs circulaires (me souviens plus du nom exacte) et excel se trompe...

Merci d'avance!

par **Sve@r** » 09 Déc 2009, 08:14

Bonjour
Les logarithmes servent à remplacer un exposant par une multiplication et une multiplication par une addition

et ln(ab)=ln(a) + ln(b)

Donc si t'as 20*A*(1,1)^A=B ça veut dire que ln(20*A*(1,1)^A)=ln(B) donc ln(20) + ln(A) + A ln(1.1) = ln(B)

Ensuite j'espère que ça peut t'aider...

par **Ben314** » 09 Déc 2009, 10:05

Si tu veut une réponse un peu plus "théorique",
On ne sait pas "résoudre" les équations de la forme

(q, a réels fixés, x=inconnue à chercher)
Evidement il faut un peu expliquer ce que signifie "résoudre" ici :
Dans certains cas particulier, il se peut que la solution "saute aux yeux" : par exemple

a pour solution

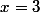, mais on ne peut pas donner la (les) solution(s) de

sous la forme x=... avec dans les point de suspension les fonction "usuelles", c'est à dire des log, exponentielles, puissances...

Par contre, connaissant q et a, en étudiant les variations de la fonction

, on peut déterminer s'il y a ou pas des solutions (et combien) puis, par exemple en utilisant une dicotomie ou le graphe de la fonction approximer ces solutions.

Dans un tableur, on peut faire faire "automatiquement" cette dichotomie au tableur pour qu'il trouve la solution de l'équation (si tu ne voit pas comment faire, on pourra t'aider)
par contre, vu les fonctions que connait le tableur, tu ne peut pas mettre dans une case une "formule" qui donne la solution (car une telle formule n'existe pas...)

par **lycfabert/rom** » 09 Déc 2009, 19:32

Salut,
Merci à vous deux pour vos réponses ! J'avais essayé de dévelloper comme tu l'explique Sve@r, mais malheuresement ça ne débouché sur rien... (dans le sens ou comme l'explique Ben314, je ne pouvais tomber sur quelque chose de la forme x= C).

Ben, donc tu sais comment résoudre cette équation avec un tableur? Peux tu m'expliquer comment s'il te plais? Tant que le tableur me donne la valeur de B en partant de A, ca peut m'etre utile.... Mais est-ce bien comme cela que marche la solution que tu me propose?
:hein: en fait, je suis pas sur d'avoir bien compris ce qu'est une dicotomie...
Je n'ais pas étudié ça encore, ou alors, c'est le nom qui ne me dit rien...

Merci beaucoup, les gars !

par **Ben314** » 11 Déc 2009, 00:10

La "dichotomie", ca consiste petit à petit à encadrer la solution d'une équation, par exemple

(q>1 et y>0 sont connus, on cherche x)
On suppose que, vu la taille max que risque d'avoir y, la solution est entre 0 et 1000.
on calcule le millieu entre 0 et 1000 : 500 et on compare f(500) avec y (où évidement f(x)=xq^x qui est une fonction croissante)
si f(500)y"
Dans la case B2 tu met "(A1+A2)/2 si A3y"
Dans la case B3 tu recopie la formule de A3 qui, comme tu l'a déplacée doit automatiquement devenir "la formule qui calcule f( (B1+B2)/2)"

Tu copie ensuite les cases B1,B2,B3 dans C1,C2,C3 jusqu'a Z1,Z2,Z3 (voire encore plus loin) normalement, les cases Z1 et Z2 donnent un encadrement assez précis du "x" que tu cherche. (si ce n'est pas assez précis, augmente la largeur du tableau)
Bien sur, une fois cela fait, tu peut "cacher" les lignes en demandant que leur hauteur soit 0.

Si ce n'est pas assez clair, redemande (en m'envoyant un message, par exemple). Je pense qu'il faut d'abord comprendre la méthode "à la main" pour comprendre la méthode sous exel.

P.S. je suis un trés piètre utilisateur d'Excel, peut être qu'il y a une solution plus simple, mais je ne connait que celle là...

par **lycfabert/rom** » 11 Déc 2009, 00:29

Merci, c'est très clair, j'ai tout compris !

Je ne savais pas que cette méthode existait, ça revient donc à faire un encadrement progressif.

Comme x ne prendra pas des valeures supérieurs à 100 (j'en doute, en tout cas pour ce que je vais en faire), le tableau ne sera pas très long...
Je m'y mettrais dès demain, merci beaucoup !

Simplification avec ln et exp

simplification avec ln et exp

Qui est en ligne