Limite d'une suite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
GPP
- Messages: 5
- Enregistré le: 19 Mai 2008, 16:14
-
 par GPP » 04 Déc 2009, 15:15
par GPP » 04 Déc 2009, 15:15
Salut tout le monde; j'ai une limite dont j'ai du mal à calculer:
Soit la suite reelle tel que Un=sqr(Un-1 +n);
on montre alors que lim Un/sqr(n)=1 et que lim Un-sqr(n)= 1/2.
On demande alors de caluler lim sqr(n)(Un-sq(n)-1/2).
Pardon j'ai oublié U0=0.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 04 Déc 2009, 15:58
par Pythales » 04 Déc 2009, 15:58
Utilise latex. C'est incompréhensible comme ça.
-
GPP
- Messages: 5
- Enregistré le: 19 Mai 2008, 16:14
-
 par GPP » 04 Déc 2009, 16:04
par GPP » 04 Déc 2009, 16:04
désolé je ne dispose pas de cet outil.
Par lim j'entend limite en plus l'infini; par Un= U(n) et par sqr racine carré. J'espère que c'est plus lisible maintenant.

-
fourize
- Membre Rationnel
- Messages: 563
- Enregistré le: 26 Oct 2008, 00:40
-
 par fourize » 04 Déc 2009, 16:45
par fourize » 04 Déc 2009, 16:45
je dirais utilise le théorème de gendarme !!
en faisant des comparaisons avec ce que t'as trouvé avant !
au passage bonsoir ;-)
* In God we trust, for all others bring data *
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 04 Déc 2009, 17:24
par Pythales » 04 Déc 2009, 17:24
Est-ce
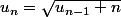
?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 04 Déc 2009, 20:17
par Ben314 » 04 Déc 2009, 20:17
Bonsoir.
Pour le 1) (déjà fait)
Je suppose que tu as montré (par récurrence) que

(ce qui implique que
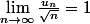
)
Pour le 2) (déjà fait)
Le 1) permet d'écrire
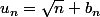
avec

et une méthode assez naturelle est d'écrire, pour
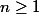
:
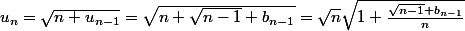
puis d'utiliser un D.L. de
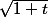
pour conclure.
Pour le 3) (indics)
Le 2) permet d'écrire
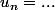
avec

telle que ... et une méthode assez naturelle est d'écrire, pour
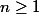
:
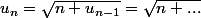
puis d'utiliser un D.L. de
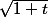
pour conclure.
En cherchant bien, je me demande s'il ne serait pas possible de rajouter une question 4), peut être même 5), voire 6).... :zen:
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 05 Déc 2009, 17:39
par Pythales » 05 Déc 2009, 17:39
Le but de l'exo est de trouver un DL de

sous forme

On trouve
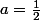
comme prévu.
Pour

j'ai trouvé
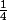
mais j'ai l'impression que c'est plutôt
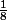

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 05 Déc 2009, 17:48
par Ben314 » 05 Déc 2009, 17:48
Bonjour, Pythales
Fait attention a ce que, avant d'écrire "je vais calculer le D.L. (en sqrt(n)) de u_n", il faudrait justifier qu'il existe...
Et je pense que tu peut le justifier uniquement en le "calculant pas à pas"
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 05 Déc 2009, 18:25
par Pythales » 05 Déc 2009, 18:25
Oui. C'est fait, mais j'ai un doute sur le coefficient de

Le calcul donne
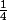
mais excel donne
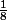
...

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 05 Déc 2009, 18:33
par Ben314 » 05 Déc 2009, 18:33
j'ai pas fait les calculs (je vais les faire) mais, juste pour être méchant, à priori, je donnerais raison à exel....
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 05 Déc 2009, 18:40
par Ben314 » 05 Déc 2009, 18:40
Je confirme : EXCELL 1 , PYTHALES 0
N'as tu pas oublié le terme d'ordre 2 dans le D.L. de sqrt(1+t) ?
(il n'est pas négligeable)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 05 Déc 2009, 18:49
par Pythales » 05 Déc 2009, 18:49
Yes soeur.
Merci...
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 07 Déc 2009, 16:17
par Pythales » 07 Déc 2009, 16:17
En "poussant" un peu le calcul, on trouve
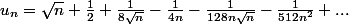
Le développement asymptotique est indépendant de la valeur de

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
 (ce qui implique que
(ce qui implique que 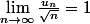 )
)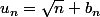 avec
avec  et une méthode assez naturelle est d'écrire, pour
et une méthode assez naturelle est d'écrire, pour 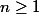 :
: 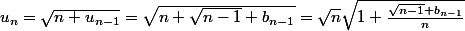
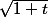 pour conclure.
pour conclure.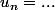 avec
avec  telle que ... et une méthode assez naturelle est d'écrire, pour
telle que ... et une méthode assez naturelle est d'écrire, pour 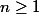 :
: 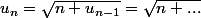
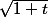 pour conclure.
pour conclure.