Bonjour, voilà je suis nouveau sur le forum et j'aurais aimé profiter de vos talents en mathématiques pour un petit problème qu'il m'est impossible de résoudre ou du moins totalement :
intégrale ( dx / (x-1)((x^3)-1))
j'ai appliqué le théoreme de la decomposition de fraction rationnelle en éléments simples mais à la fin je me retrouve avec deux fractions dont les primitives sont simples mais ou la troisième s'avère complexe ( en français :id: ) ... du genre :
int ( (-1) / (x-1)) + int ( 1/ 3(x-1)^2) + int ((3x-1)/3(x^2+x+1))
voilà voilà merci d'avance pour vos réponses !!!!
Intégrale et décomposition
10 messages
- Page 1 sur 1
La dernière intégrale est dite "du type machin-chose" (j'ai oublié le nom)
Pour la calculer, il faut mettre le dénominateur sous la forme 1+(?x+?)^2
(c'est plus ou moins la forme canonique d'un poly du second degrés) puis fair un changement de variable t=?x+? pour que le dénominateur soit 1+t^2. Enfin, il faut un peu de culture :
Primitive de 1/(1+t^2) => ???
Primitive de t/(1+t^2) => ???
ca roule ?
Pour la calculer, il faut mettre le dénominateur sous la forme 1+(?x+?)^2
(c'est plus ou moins la forme canonique d'un poly du second degrés) puis fair un changement de variable t=?x+? pour que le dénominateur soit 1+t^2. Enfin, il faut un peu de culture :
Primitive de 1/(1+t^2) => ???
Primitive de t/(1+t^2) => ???
ca roule ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Alors d'abord merci pour ta réponse, mais bon tu ne parle pas à un prépa en maths spé étoile là :id: ce que je veux dire c'est que pour la culture ça je pense que c'est bon, la première doit être l'arctan et la seconde 1/2 ln((x^2)+1) si je ne me trompe pas, mais pour la forme canonique et le changement de variable j'ai un peu plus de mal...pourrait tu m'expliquer un peu plus sans voulour abuser de ton temps. ( PS : ne penser en aucun cas que je suis un faigneant qui vous utilise pour faire ses exos pendant que je me la coule douce, j'ai passé deux jours sur cette feuille d'exo et que j'ai plusieurs petits exo comme cela où un petit détail m'échappe ce qui m'empeche de le résoudre totalement...) Merci encore .
la "forme canonique" :
^2-{\Delta \over 4a^2}])
et, dans le contexte, est forcément strictement négatif, sinon on pourait factoriser et donc réduire en deux éléments plus simples...
est forcément strictement négatif, sinon on pourait factoriser et donc réduire en deux éléments plus simples...
on factorise alors dans le crochet :
dans le crochet :
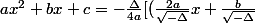^2+1])
Ensuite, si tu n'est pas trop familier avec les changement de variables dans les primitives tu peut te poser la question sous la forme :
Pour quel(s) type(s) de numérateurs suis-je capable de trouver une primitive de^2+1})
et, dans le contexte,
on factorise alors
Ensuite, si tu n'est pas trop familier avec les changement de variables dans les primitives tu peut te poser la question sous la forme :
Pour quel(s) type(s) de numérateurs suis-je capable de trouver une primitive de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
sniffff, je vais pleurer je crois !!!! :triste: j ai réussi à factoriser le dénominateur sous la forme (kx+c)^2 +1 mais jamais au numérateur je pourrais retrouver en changeant de variable (kx+c)' ...bref j ai deux autre questions : la première sur cette expression :
int ( arcsin ( (2x)/((x^2)+1)))dx
1) si on pose x=tan u en changement de variable à t on le droit ensuite de dire que u= x/2 ce qui m arrangerai fortement pour utiliser la formule de l'arc moitié...
2) dans l'expression de l'intégrale , "dx" est en dehors de la parenthèse de "arcsin" à t on le droit de l'intégrer dans la parenthèse ??? Car si non dans le changement de variable x=tan u on devra dire que du=(dx/((x^2)+1)) or comment exprimer cela si dx ne peut être intégrer à la parenthèse????
Merci d'avance...
int ( arcsin ( (2x)/((x^2)+1)))dx
1) si on pose x=tan u en changement de variable à t on le droit ensuite de dire que u= x/2 ce qui m arrangerai fortement pour utiliser la formule de l'arc moitié...
2) dans l'expression de l'intégrale , "dx" est en dehors de la parenthèse de "arcsin" à t on le droit de l'intégrer dans la parenthèse ??? Car si non dans le changement de variable x=tan u on devra dire que du=(dx/((x^2)+1)) or comment exprimer cela si dx ne peut être intégrer à la parenthèse????
Merci d'avance...
Ne tournons pas autour du pot : il y a DEUX fractions avec (kx+c)^2+1 au dénominateur que l'on sait "primitiver" :
^2+1) => une primitive est
=> une primitive est )
\over (kx+c)^2+1) => une primitive est
=> une primitive est ^2+1))
A l'aide de ces deux là, on peut trouver les primitives de toutes les fonctions de la forme^2+1)
On peut aussi, comme le dit si bien alavacommejetepousse, commencer par enlever les "x" (en "faisant apparaitre" un u'/u de primitive ln(u)) avant de mettre sous forme canonique le dénominateur : dans ce cas il ne restera que la primitive de forme "arctan".
C'est comme on veut.
A l'aide de ces deux là, on peut trouver les primitives de toutes les fonctions de la forme
On peut aussi, comme le dit si bien alavacommejetepousse, commencer par enlever les "x" (en "faisant apparaitre" un u'/u de primitive ln(u)) avant de mettre sous forme canonique le dénominateur : dans ce cas il ne restera que la primitive de forme "arctan".
C'est comme on veut.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
hihihih Ben314 tu va me tuer mais y'a pas moyen je bloque là :hum: !!! enfaite ça fait tellement longtemps que je suis sur cet exo que je sature, mon cerveau il bloque là !!!! Du coup je conçois ton idée des deux primitives connues mais avec le numérateur que j'ai je n'arrive pas à faire le lien avec le dénominateur : allez je te dis ce que j'ai pour voir si c'est moi qui ai un problème où alors qu'il y a vraiment un souci : j'ai (x+(1/3))/(((2*sqrt(3))/3)x+((2*sqrt(3))/3)^2+1)
Voilà si tu pouvais me filer le petit déclic ce serait super sympa !!!
Voilà si tu pouvais me filer le petit déclic ce serait super sympa !!!
tu utilise la fonction qui a pour primitive le ln(...) pour faire disparaitre les x
L'idée et que, si tu veux du 2X+3 alors que tu as du 3X+5, tu "force le destin" en écrivant 3X+5=3/2.(2X+3)-9/2+5... (c'est ce que te disait alavacommejetepousse).
ensuite il te reste une constante (au numérateur) et c'est gagné.
L'idée et que, si tu veux du 2X+3 alors que tu as du 3X+5, tu "force le destin" en écrivant 3X+5=3/2.(2X+3)-9/2+5... (c'est ce que te disait alavacommejetepousse).
ensuite il te reste une constante (au numérateur) et c'est gagné.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
