[DM maths]équation du second degré
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
vax
- Messages: 4
- Enregistré le: 04 Nov 2009, 09:20
-
 par vax » 04 Nov 2009, 09:25
par vax » 04 Nov 2009, 09:25
bonjour a tous je suis éleve en classe de première et je bloque sur une question de mon DM de maths:
soit (E) l'équation d'inconnue x: (m-1)x²-4mx+m-6=0 , où m est un paramètre réel
déterminer m pour que (E) ne soit pas une équation du second degré et résoudre alors (E)
sa fait une semaine que je bloque la dessus
aidez moi svp
merci
-
dudumath
- Membre Relatif
- Messages: 417
- Enregistré le: 18 Nov 2007, 11:04
-
 par dudumath » 04 Nov 2009, 09:27
par dudumath » 04 Nov 2009, 09:27
Pour que l'équation ne soit pas du second degré, il faut qu'il n'y ait pas de terme en x²...
donc la seule valeur de m qui convient est m=...?
-
vax
- Messages: 4
- Enregistré le: 04 Nov 2009, 09:20
-
 par vax » 04 Nov 2009, 09:29
par vax » 04 Nov 2009, 09:29
dudumath a écrit:Pour que l'équation ne soit pas du second degré, il faut qu'il n'y ait pas de terme en x²...
donc la seule valeur de m qui convient est m=...?
est-ce que c'est m=1?
-
dudumath
- Membre Relatif
- Messages: 417
- Enregistré le: 18 Nov 2007, 11:04
-
 par dudumath » 04 Nov 2009, 09:30
par dudumath » 04 Nov 2009, 09:30
tout à fait, donc avec m=1 tu obtiens une équation du 1er degré facile à résoudre ;)
-
vax
- Messages: 4
- Enregistré le: 04 Nov 2009, 09:20
-
 par vax » 04 Nov 2009, 09:31
par vax » 04 Nov 2009, 09:31
ok merci j'y crois pas que je sois passer a coté de ça
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 04 Nov 2009, 09:34
par benekire2 » 04 Nov 2009, 09:34
la question d'après n'est pas de déterminer en fonction des valeurs de m le nombre de solutions de l'équation ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 04 Nov 2009, 09:35
par Dinozzo13 » 04 Nov 2009, 09:35
x^2-4mx+m-6=0)
Selon le cours dee 1re S sur le trinôme, tu dois distinguer deux cas :

et

.
1°) Pour
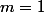
, tu résous l'équation en remplaçant m par cette valeur.
2°) Pour

, tu appliques la formule du trinôme, tu calcules le discriminant.
Une fois arrivé là, tu étudie son signe.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 04 Nov 2009, 09:38
par benekire2 » 04 Nov 2009, 09:38
oui et le nombre de solution dans le cas ou m ne fait pas 1 dépendra de ton discriminant...
-
vax
- Messages: 4
- Enregistré le: 04 Nov 2009, 09:20
-
 par vax » 04 Nov 2009, 09:50
par vax » 04 Nov 2009, 09:50
benekire2 a écrit:la question d'après n'est pas de déterminer en fonction des valeurs de m le nombre de solutions de l'équation ?
eeeee non pas vraiment la question d'après c'est:
on suppose désormais que (E) est du second degré. déterminer m dans chacun des cas suivant
a)-1 est racine de (E)
b)(E) admet une racine double
c)(E) n'admet pas de racines réelle
d)(E) admet deux racines de signe opposés
e) pour tout réel x, (m-1)x²-4mx+m-6<0
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
