Exercice suite

par **psykanel** » 01 Nov 2009, 18:23

Bonjour a tous voilà mon exercice

soit Pn+1 un nombre d'individus au temps n+1

Pn+1 = a.Pn.e^(-b.Pn)

avec a et b des constantes telles que a>1 et b>0

1)vérifier que la suite Pn est croissante si et seulement si Pn =< lna/b pour tout n
2) on suppose que Pn est convergente, soit P = lim (en l'infini)Pn. Déterminer les valeurs possibles de P.

Pour la 1) je pense a mettre cette suite sous forme de fonction, ensuite en calculer la dérivée pour en déduire le sens de variation de la fonction.

suis-je sur la bonne voi ?

après calcul de la dérivée je devrai donc trouver que celle-ci s'annule en lna/b ? :doh:

par **zerkel** » 01 Nov 2009, 19:02

bonsoir,
as-tu vu en cours la méthode qui consiste à étudier le quotient

et de le comparer à 1 lorsque ta suite a des termes strictement positifs? (tu peux étudier le cas où la suite est constante égale à 0 à part)

Sinon concernant ton idée je ne suis pas convaincue qu'elle puisse aboutir car il me semble en général que lorsque l'on étudie la fonction f c'est dans le cas où l'on a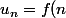

et là ce que tu as c'est

.

par **Ericovitchi** » 01 Nov 2009, 19:06

C'est plus compliqué que ça.
la dérivée s'annule en 1/b et pas en lna/b

Pour comprendre le phénomène de croissance ou pas de la suite, il faut tracer la courbe y=x et voir où elle coupe la courbe. Si le point Pn est après ce point alors la suite décroit alors que s'il est avant elle croît (les points Pn rebondissent alternativement sur la courbe et sur la droite y=x. Tu as vu ça en cours ?)
C'est en calculant ce point d'intersection (en faisant

) que l'on trouve la fameuse valeur lna/b

par **zerkel** » 01 Nov 2009, 19:15

cela fait très longtemps que j'ai eu mon dernier cours sur les suites récurrentes, mais je pense que ma méthode est plus simple si elle a été vue dans ton cours, parce que tu te retrouves juste à résoudre une inéquation et tu trouves le résultat très rapidement est faisant attention aux changements de sens dans les inégalités.

par **zerkel** » 01 Nov 2009, 19:20

en fait non cela revient au même point de vue difficulté. Mais comme je n'ai pas de livre avec le cours à côté ma méthode me semble plus simple...

par **psykanel** » 01 Nov 2009, 19:21

merci pour vos réponses enfaite je me suis un peut embrouillé les idées avec cette histoire de dérivé, j'ai cherché la complication alors que tout est évident
en calculant Pn+1/Pn>=1
on arrive a la réponse attendu =)
je passe a la question 2

par **psykanel** » 01 Nov 2009, 19:44

pour se qui est de la question 2:
lim(+infini) Pn = 0 puisque la suite Pn est décroissante avec Pn >= lna/b et qu'une population ne peut etre négative. Cependant je ne vois pas pourquoi on me demande LES valeurs de P?

par **zerkel** » 01 Nov 2009, 19:53

on a vu que la suite est CROISSANTE ssi

par **psykanel** » 01 Nov 2009, 20:05

je sais bien mais si la suite converge je ne voit pas d'autre solution

par **zerkel** » 01 Nov 2009, 20:14

Et si

, cela donne quoi?
(Je n'ai pas réfléchi encore aux autres possibilités, mais bon là déjà cela te donne une deuxième réponse)

par **psykanel** » 01 Nov 2009, 20:26

le but est bien de calculer la limite en + ?
je tombe sur 0, alors si tu pouvais m'expliquer comment tu arrive a une autre solution ?

par **zerkel** » 01 Nov 2009, 21:33

et bien justement étudie la suite si le premier terme est celui que j'ai donné dans le message précédent. Calcule

. Que constates-tu?

par **psykanel** » 02 Nov 2009, 16:52

désolé pour le retard
si P0= lna/b
on a P1=lna/b=P0
alors P0=P1=P2=Pn
donc la suite peut également être constante :id:

Exercice suite

exercice suite

Qui est en ligne