Exercice limites de suites TS

par **lilou-marmotte** » 26 Oct 2009, 22:45

Bonjour tout le monde
Donc voilà, j'ai un petit exercice type bac à faire et j'aurais besoin d'un peu d'aide ou simplement d'être rassurée. =)
__________________________________________________

La suite (Un) est définie pas U0=0 et par la relation de récurrence:
Un+1=(2U(n)+3)/(U(n)+4)

1. Calculer U1 et U2
2. Montrer que, pour n>0:
03. On pose, pour nN (: appartient ^^):
Vn=(U(n)-1)/(U(n)+3)
Montrer que (Vn) est géométrique convergente.
4. Calculer (Un) en fonction de Vn.
En déduire que (Un) converge et déterminer sa limite.
__________________________________________________

pour la 1:
U1=3/4
U2=18/19

pour la 2:
j'ai tenté la récurrence mais ça n'aboutit pas vraiment:

Soit la proposition p(n): n>0 0U1=3/4
0p(1) vraie

Considérons un entier P(p) tel que p>p(1) et P(1) vraie
P(p+1) est- elle vraie?

00<2U(1)<2
3<2U(1)+3<5
...
mais pour finir, ça va pas;
12/19 < U2 < 20/19

Je ne sais donc pas quoi faire ^^'

un petit coup de main?
Merci :happy2:

par **Dinozzo13** » 26 Oct 2009, 23:02

Pour la 1., il n'y aucune difficulté.
Pour la 2., tu as vu juste, il faut bien faire un raisonement par récurrence.

par **lilou-marmotte** » 27 Oct 2009, 07:44

oui mais justement, le problème c'est que je n'arrive pas à faire ma récurrence ^^'

par **Dinozzo13** » 27 Oct 2009, 11:36

bah pour commencer, essaye le cas

. Supposons que

, montrons alors que

. D'après l'yhpotèse de récurrence :

A partir de cette inégalité, tu peux encadrer le numérateur et le dénominateur de

, tu en déduis donc un encadrement de

, tu conclus, voilà, c'est fini.

par **lilou-marmotte** » 27 Oct 2009, 12:10

c'est ce que j'ai fait ^^
Mais je n'atterrit pas sur 0mais sur 12/19 < Un+1 < 20/19
C'est ça qui me gène lol

par **Dinozzo13** » 27 Oct 2009, 17:33

eh bien,

donc tu peux exprimer le numérateur :

, et le dénominateur :

tu en déduis donc que :

, à toi :we: .

par **lilou-marmotte** » 27 Oct 2009, 17:37

ha mais oui haha
je n'avais pas pensé à les séparer l'un de l'autre ^^
pour 0Y a des jours ou jme sens nouille xD

Un GRAND merci, je vais développer ca et le mettre par écrit.

Pour le 3. Je dois remplacer Un, dans Vn?

par **Dinozzo13** » 27 Oct 2009, 17:55

t'inquiète je vais t'aider :zen: .
Pour montrer que

est géométrique, il faut calculer

, simplifier au max, puis essayer de l'exprimer en fonction de

, car d'après le cours,

est géométrique ssi

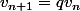
avec

la raison.

par **lilou-marmotte** » 30 Oct 2009, 15:46

et comment on calcule V(n+1)?

par **jameso** » 30 Oct 2009, 15:59

V(n+1)=(U(n+1)-1)/(U(n+1)+3)

Remplace alors U(n+1) par sa valeur dans l'expression ci-dessus et après quelques calculs tu vas voir que ta suite V(n) est géométrique de raison :à toi de trouver....

par **Dinozzo13** » 30 Oct 2009, 19:38

je peux proposer un correction, si vous le souhaitez.

par **lilou-marmotte** » 30 Oct 2009, 20:28

Merci ^^
J'ai réussi impec, raison=1/5
J'ai aussi prouvé que Vn est convergente

4. Pour trouver Un, je pars donc de Vn mais je trouve n'importe quoi xD
3Vn/(3V(n)²+2V(n)+1)

Exercice limites de suites TS

Exercice limites de suites TS

Qui est en ligne