Fonctions
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
micka
- Membre Naturel
- Messages: 87
- Enregistré le: 02 Oct 2006, 14:27
-
 par micka » 18 Oct 2009, 14:55
par micka » 18 Oct 2009, 14:55
Bonjour j'ai des doutes sur l'ensemble de définition d'une fonction .
Une fonction f définie par f(x) =( x²+4x)/2(x²+2)
Justifier l'ensemble de définition Df : je trouve : R - {-V2 ; V2 } ?
Résoudre f(x) >= 0
tableau de signe : - l'infini , - 4 , - V2 , 0 , V2 , + l'infini
x
x+4
2
x + V2
x - V2
f(x)
Qu'en pensez-vous ?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 18 Oct 2009, 15:07
par Ericovitchi » 18 Oct 2009, 15:07
Tiens pourquoi enlever les deux valeurs -V2 ; V2 ?
Elles n'annulent pas le dénominateur.
-
micka
- Membre Naturel
- Messages: 87
- Enregistré le: 02 Oct 2006, 14:27
-
 par micka » 18 Oct 2009, 15:17
par micka » 18 Oct 2009, 15:17
Ensemble de définition R ?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 18 Oct 2009, 15:19
par Ericovitchi » 18 Oct 2009, 15:19
oui, le dénominateur n'est jamais nul, donc le domaine de définition est R
-
micka
- Membre Naturel
- Messages: 87
- Enregistré le: 02 Oct 2006, 14:27
-
 par micka » 18 Oct 2009, 15:22
par micka » 18 Oct 2009, 15:22
Merci bien donc pour le tableau de signe ca donne :
- l'infini , - 4 , - 2 , 0 , + l'infini
x
x+4
2
x² +2
f(x)
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 18 Oct 2009, 15:23
par oscar » 18 Oct 2009, 15:23
Bonjour
f(x) = (x² + 4x) / 2 (x²+2)
Domf = R
Racines 0 et -4
f(x) >0 dénominateur toujours >0
Etude de f(x) >0
x.............-4..........0.........
f(x) Signes,,............................. ??
On ne doit pas calculer f' (x)

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 18 Oct 2009, 15:25
par Ericovitchi » 18 Oct 2009, 15:25
la ligne avec le 2 est inutile
et la valeur -2 en colonne, elle sert à quoi ?
-
micka
- Membre Naturel
- Messages: 87
- Enregistré le: 02 Oct 2006, 14:27
-
 par micka » 18 Oct 2009, 15:29
par micka » 18 Oct 2009, 15:29
Oui effectivement je voie ou est mon problème . J'avais tout autre chose en tête .
-
micka
- Membre Naturel
- Messages: 87
- Enregistré le: 02 Oct 2006, 14:27
-
 par micka » 18 Oct 2009, 15:32
par micka » 18 Oct 2009, 15:32
Ca nous donne bien : ] - l'infini ; -4 ] U [ O ; + l'infini [ ?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 18 Oct 2009, 15:35
par Ericovitchi » 18 Oct 2009, 15:35
oui c'est exact
-
micka
- Membre Naturel
- Messages: 87
- Enregistré le: 02 Oct 2006, 14:27
-
 par micka » 18 Oct 2009, 15:36
par micka » 18 Oct 2009, 15:36
Ok merci bien de m'avoir remis sur le bon chemin .
-
micka
- Membre Naturel
- Messages: 87
- Enregistré le: 02 Oct 2006, 14:27
-
 par micka » 18 Oct 2009, 15:44
par micka » 18 Oct 2009, 15:44
Mais il y a quelque chose que je ne comprends pas trop voila on a comme dénominateur x² +2 donc l'ensemble de définition c'est R - {-V2 ; V2 } vu qu'il faut x² +2 différent de 0 donc x différent de V2 et - V2 . Ou mieux que cela s'applique que pour les dérivés ?
Désolé les fonctions n'ont jamais était mon point fort :(

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 18 Oct 2009, 15:55
par Ericovitchi » 18 Oct 2009, 15:55
x² +2 =0 n'entraine pas x =
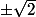
x²+2=0 --> x²=-2 et un carré ne peut jamais être négatif.
Si tu avais eu x² -2 au dénominateur alors tout ce que tu dis aurait été exact
-
micka
- Membre Naturel
- Messages: 87
- Enregistré le: 02 Oct 2006, 14:27
-
 par micka » 18 Oct 2009, 16:00
par micka » 18 Oct 2009, 16:00
Sincèrement merci tu viens de répondre à une question dont je me posé depuis un bon moment .
-
micka
- Membre Naturel
- Messages: 87
- Enregistré le: 02 Oct 2006, 14:27
-
 par micka » 18 Oct 2009, 16:10
par micka » 18 Oct 2009, 16:10
Heu tant que je t'ai sous la main :) est ce que tu peux me dire si u'(x) est bien égale à 2x +4 et v'(x) est bien égale à 2x s'il te plait :) c'est pour la dérivé

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 18 Oct 2009, 16:18
par Ericovitchi » 18 Oct 2009, 16:18
oui u'=2x+4
v'=4x car le dénominateur est 2(x²+2)
-
micka
- Membre Naturel
- Messages: 87
- Enregistré le: 02 Oct 2006, 14:27
-
 par micka » 18 Oct 2009, 16:23
par micka » 18 Oct 2009, 16:23
Ok merci bien , par contre je pense qu'il faut développer car je voie rien qui peut se factoriser :s (2x+4) * 2 (x²+2 ) - ( x²+4x) * 4 x / 4(x²+2 )²
Je ne me trompe pas ? il faut bien développer ?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 18 Oct 2009, 16:26
par Ericovitchi » 18 Oct 2009, 16:26
oui il faut développer, mais ça va s'arranger. le numérateur peut s'écrire -8 (x-2) (x+1)
-
micka
- Membre Naturel
- Messages: 87
- Enregistré le: 02 Oct 2006, 14:27
-
 par micka » 18 Oct 2009, 16:37
par micka » 18 Oct 2009, 16:37
Oui tout à fait , infiniment merci de tes réponses :)
-
micka
- Membre Naturel
- Messages: 87
- Enregistré le: 02 Oct 2006, 14:27
-
 par micka » 18 Oct 2009, 16:45
par micka » 18 Oct 2009, 16:45
f' à donc le signe de ( x+2 ) ( x- 1 ) ?
Donc Si x appartient ] - l'infini ; -2 [ U ] 1 ; + l'infini [ alors f'(x) >0
Si x appartient ]-2 , 1 [ alors f'(x) <0
Si x = -2 ou x = 1 alors f'(x) = 0
Je me suis pas trompé ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
