Coordonnée d'un point

[maxime59000]

Bonjour, je suis bloqué dans une question de mon DM de maths. Je vous ai mis la question sur laquelle je coince :


on considère les points (A(5;2) B(4;-2) C(8;-3) D(9;1). Sachant que le quadrilatére ABCD est un carré, calculer les coordonnées du point M tel que MA+2MB-MC+3MD=0.

Ce sont des vecteurs.


Merci =)

[mathelot]

bonsoir,

quand on est confronté à ce genre de somme (on appelle ça une combinaison linéaire de vecteurs) , on doit se poser
toujours une question. :doh:

laquelle ?

(as-tu étudié la fonction de Leibniz ?)

bio de Leibniz

[oscar]

Bonsoir

Calcule les coordonnées

de v MA =( x-5;y-2)
de +2 v MB=
de - 2 V MC=
de + 3 V MD =


de la somme obtenue

Compare avec O ( o ; o)

Détermine ( x;y)

[mathelot]

re,

pas de réponse. :hum:

on peut regarder si la somme des coefficients de la combinaison linéaire est nulle: 1+2-1+3=5

elle ne l'est pas.
d'où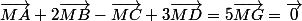

M est en G, barycentre de A(1),B(2),C(-1),D(3)

on place A' aux deux tiers de [AB]
C' le milieu de [A',D]
M barycentre de C'(6) et C(-1)

[benekire2]

Il suffit d'utiliser les coefficients barycentriques, de la forme : x= (axA+bxB+cxC+dxD)/(a+b+c+d) et y = ....