La continuité d'une application
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
lost-_-
- Membre Naturel
- Messages: 17
- Enregistré le: 12 Fév 2009, 21:06
-
 par lost-_- » 10 Oct 2009, 12:52
par lost-_- » 10 Oct 2009, 12:52
Bonjour,
J'ai besoin de votre aide afin de résoudre cet exo :
on a une application f définie comme suit:
f: R² -> R
(x,y) -> xy
(respectivement de C² dans C)
Etudier la continuité de cette application.
(Indication: on peut considérer dans R² la distance :
d((x,y),(x0,y0))= sup (|x-x0|,|y-y0|)
Merci d'avance :happy2:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 10 Oct 2009, 12:59
par Nightmare » 10 Oct 2009, 12:59
Salut !
Et donc? Qu'est-ce que tu n'arrives pas à faire?
-
lost-_-
- Membre Naturel
- Messages: 17
- Enregistré le: 12 Fév 2009, 21:06
-
 par lost-_- » 10 Oct 2009, 14:29
par lost-_- » 10 Oct 2009, 14:29
Salut,
On a d((x,y),(x0,y0))= sup (|x-x0|,|y-y0|)
On suppose que d((x,y),(x0,y0))< ;) et on cherche à prouver que cette supposition implique d(f(x,y),f(x0,y0)< ;)
on a On suppose que d((x,y),(x0,y0)) < ;)
donc sup (|x-x0|,|y-y0|) < ;)
donc |x-x0|<;) et |y-y0|<;)
je m'arrete ici
....??????????
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 10 Oct 2009, 14:45
par Nightmare » 10 Oct 2009, 14:45
Attention !! Ton application est un champ scalaire : à valeur dans R, on a donc pas la même distance sur l'ensemble d'arrivé et l'ensemble de départ !
-
lost-_-
- Membre Naturel
- Messages: 17
- Enregistré le: 12 Fév 2009, 21:06
-
 par lost-_- » 10 Oct 2009, 14:47
par lost-_- » 10 Oct 2009, 14:47
Pardon, j'ai pas saisi ce que vous avez dit..
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 10 Oct 2009, 15:02
par Nightmare » 10 Oct 2009, 15:02
Tu as écrit qu'on souhaite montrer que pour tout e blablabla "d((x,y),(x0,y0)) < a => d(f(x,y),f(x0,y0)) < e
Dis moi, que veut dire "d(f(x,y),f(x0,y0))" ?
-
lost-_-
- Membre Naturel
- Messages: 17
- Enregistré le: 12 Fév 2009, 21:06
-
 par lost-_- » 10 Oct 2009, 15:13
par lost-_- » 10 Oct 2009, 15:13
pour établir la continuité d'une application d'un espace métrique à un autre
il faut vérifier que la distance entre les coordonnées inférieur à ;), implique que la distance entre leurs images est inférieur à ;)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 10 Oct 2009, 15:15
par Nightmare » 10 Oct 2009, 15:15
Oui, ok, c'est la définition. Sauf que la métrique (ou distance si tu préfères) peut différer entre les deux espaces métriques.
Dans ton cas, tu sembles supposer qu'on munie R² et R de la même distance d. Je te demande donc quelle est la signification de d dans R !
-
lost-_-
- Membre Naturel
- Messages: 17
- Enregistré le: 12 Fév 2009, 21:06
-
 par lost-_- » 10 Oct 2009, 16:06
par lost-_- » 10 Oct 2009, 16:06
Je pense que puisque on est dans R² , on peut passer à la norme.
Dans R² en tant que l'espace du départ d((x,y),(x0,y0))= sup (|x-x0|,|y-y0|)
Dans R en tant que l'espace d'arrivée d(f(x,y),f(x0,y0))=|xy - x0.y0|
-
lost-_-
- Membre Naturel
- Messages: 17
- Enregistré le: 12 Fév 2009, 21:06
-
 par lost-_- » 10 Oct 2009, 16:22
par lost-_- » 10 Oct 2009, 16:22
un ami à établié cette inégalité :
|xy - x0.y0|< ;) (;) + |x0| + |y0| )
et il en a déduit qu'il suffit de prendre ;) = inf ( 1 , ;)/(1 + |x0| + |y0|) )
pour l'inégalité c'est bon, on peut la conclure en utilisant le fait que |x-x0|<;) et |y-y0|<;) ,
Mais pour la valeur de ;) , je ne vois pas du tout comment l'établir...
Merci
-
lost-_-
- Membre Naturel
- Messages: 17
- Enregistré le: 12 Fév 2009, 21:06
-
 par lost-_- » 10 Oct 2009, 22:56
par lost-_- » 10 Oct 2009, 22:56
j'ai vraiment besoin d'aide, en attendant votre réponse... :cry:
-
lost-_-
- Membre Naturel
- Messages: 17
- Enregistré le: 12 Fév 2009, 21:06
-
 par lost-_- » 11 Oct 2009, 12:09
par lost-_- » 11 Oct 2009, 12:09
up!! :help:
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 11 Oct 2009, 12:18
par Finrod » 11 Oct 2009, 12:18
Vérifie que
+y_{0}(x-x_{0})|)
majore par la somme des valeurs absolues, puis utilise le fait que x et
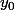
sont bornés.
Le truc avec le

ne m'inspire personnellement pas des masses.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
