Petites notions

[mad07]

bonsoir,

Je me permets de poster cette discussion pour savoir si quelqu'un pourrait m'expliquer les différences entre la dérivée d'une fonction et la différentielle de cette même fonction. Qu'est-ce qui les différencie ?
Merci d'avance, car cette incompréhension m'empêche de bien saisir et retenir mon cours
=)

[skilveg]

Bonsoir,

La principale différence c'est que la notion de dérivée n'a de sens qu'en dimension 1, alors que celle de différentielle marche en toute dimension. En dimension 1, la dérivée en un point représente le coefficient directeur de la tangente, ce qui revient à écrire .

En dimension quelconque, on approche le graphe de la fonction par son plan tangent (imagine-le pour une fonction de dans : le graphe est une nappe, qui a en tout point un plan tangent). Ce qui veut dire qu'en tout point, il y a une application affine qui approche la fonction à l'ordre 1; mathématiquement, ça s'écrit où 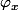est une application linéaire. C'est cette application linéaire qu'on appelle différentielle de en et qu'on note (ou , ou , ce qui autorise à noter l'approximation linéaire comme en dimension 1: ).

Le lien avec la dérivée (en dimension 1 donc) c'est que pour une fonction de dans , la différentielle en un point est une application linéaire de dans lui-même, qui est donc la multiplication par un réel: le nombre dérivé.

En espérant ne pas avoir été trop confus et avoir répondu en partie à ta question...

[mad07]

eh bien merci pour cette réponse, qui bien qu'un peu compliquée, m'a permi de saisir certaines notions jusque là assez..."floues" ^^

encore merci et bonsoir