DM sur les limites

par **boby124** » 30 Sep 2009, 13:06

Bonjour. Les premiers devoirs maison arrivent et j'aurais besoin d'aide/de correction pour ce premier.

Exercice 1 :
Il y a une limite que je n'arrive pas trouver qui est

limite en +;) de g(x)= (x+2;)x) / (3x +1)
Elle se simplifie par 2;)x/3x mais ce sont deux formes indéterminées ...

Exercice 2 :

Une fonction g est définie sur ]0;+;)[, telle qui lim g en 0 = -;), et lim g en +;) = +;).

La fonction f(x)=(x-1)+(x²+1)

on donne h=gof

1.Déterminer Dh. J'ai trouvé ]0;+;)[
2.Déterminer les limites de h aux bornes de son ensemble de definition.
Par composée, lim de f en 0 est -1, mais lim en -1 de g n'est pas calculable puisque ça ne correspond pas à son ensemble de definition?

en +;), j'ai trouvé comme réponse +;).

3.Déterminer le sens de variation de f sur Dh et en déduire celui de h

j'ai trouvé que f était stric. croissante sur ]0;+;)[
pour tout x de cet intervalle, f(x) appartient à ]-1;+;)[
cet inervalle ne correspond de nouveau pas à celui de g, je suis complètement bloqué...

En vous remerciant d'avance!!

Le premier exercice a été résolu mais je suis toujours en panne pour le deuxieme... Besoin d'aide!!

par **geegee** » 30 Sep 2009, 13:16

Bonjour,

Lorsqu'on a A(x)/B(x) la limite en +inf est le plus haut terme en x de A / le plus haut terme en x de B .

Le plus haut terme en x de

est x
Le plus haut terme en x de

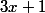
est 3x.

On a que la limite de

en + inf est la meme que la limite de

qui vaut 1/..

par **boby124** » 30 Sep 2009, 13:32

la limite de x en +;) est +;), ce qui fait +;)/+;)n de nouveau, non ?

je ne pensais que l'on pouvait autant simplifier, encore plus que 2 racine de x

donc si on simplifie encore plus ça donne 1/3, donc limite = 0 , c'est ça ?

par **geegee** » 30 Sep 2009, 13:53

Bonjour,

Oui cela donne 1/3 et limite en +inf de 1/3 est la meme chose d'ou le resultat est 1/3.

par **geegee** » 30 Sep 2009, 14:01

Bonjour,

pour l'exercice 2 cela est correct en 0 cela fait f( 0 ) =0 et gof(0)= -inf
f( +inf) =+inf gof(+inf)= +inf

par **boby124** » 30 Sep 2009, 14:05

Merci beaucoup.

Mais je ne comprend pas comment trouver la limite de gof en 0 puisque la limite de f en 0 est -1 et que pour trouver celle de gof en 0 il faut passer par celle de g en -1, qui n'existe pas

par **geegee** » 30 Sep 2009, 14:25

Bonjour,

Comme f(x)=(x-1)+(x²+1)
f(0) = (0-1)+(0²+1) =....
Non ?

par **boby124** » 30 Sep 2009, 14:45

effectivement, faute idiote de calcul qui fausse tout...

par **geegee** » 30 Sep 2009, 15:11

Rebonjour,

De toute facon le résonnement était correct.

par **boby124** » 30 Sep 2009, 15:15

Merci beaucoup!

par **boby124** » 30 Sep 2009, 15:26

ah mais non je ne m'étais pas trompé

f(x) = (x-1 ) / (x²+1)
et non +

DM sur les limites

DM sur les limites

Qui est en ligne