Bonjour !! Je t'engage à aller lire d'urgence le réglement !!
Je suis actuellement sur un exercice de mathématiques dont l'énoncé est le suivant :
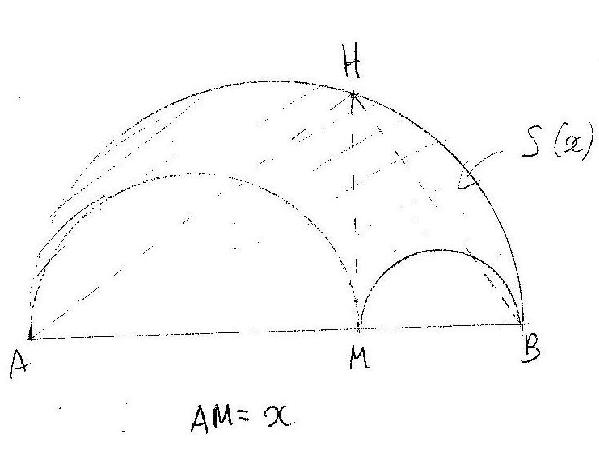
"On note S(x) l'aire (hachurée, voir image attachée) limitée par les 3 demi-cercles respectifs [AB], [AM] et [MB].
On suppose que AB = 10 et AM = x (0x10)
Partie A : Calcul de S(x)
Vérifier l'égalité S(x) = /4 x (10-x)
Trouver le maximum de S(x) revient alors à trouver celui de f(x) = x(10-x)
L'exercice demande alors dans la partie B de trouver ce maximum de 2 manières : une 1ère méthode algébrique (qui ne pose pas ici de problèmes) et une 2ème partie géométrique avec 3 questions qui me posent problème .
Voici les questions :
La perpendiculaire à (AB) en M coupe le demi cercle de diamètre [AB] en H.
a) Montrer que l'angle MAH est égal à l'angle MHB
b) En utilisant la tangente de ces angles, établir que MH² = f(x)
c) Résoudre alors le problème posé (trouver le maximum de S(x))
L'exercice me semble cependant pas très précis car pour l'égalité d'angle il devrait être précisé "pour x donné" car pour certaines valeurs de x cette égalité est fausse. Il parait évident visuellement que ces 2 angles sont égaux mais je n'arrive pas à le justifier.
Merci d'avance pour votre aide.
