Devoir maison de mathématiques (fonctions, barycentres.)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
SteezyRider
- Membre Naturel
- Messages: 17
- Enregistré le: 29 Sep 2010, 15:28
-
 par SteezyRider » 20 Oct 2010, 14:39
par SteezyRider » 20 Oct 2010, 14:39
Bonjour,
J'ai ce DM de mathématiques à faire, je suis en 1ère S.

Uploaded with
ImageShack.usJe ne comprends pas l'exercice 1 (pour les autres, je n'ai pas très bien regardé mais je pense que je pourrais y arriver).
Je sais qu'il faut faire un système avec les deux équations pour trouver quel serait les intersections, mais nous n'avons pas encore vu ce genre de fonction.
Comment pourrais-je faire ?
Merci d'avance
Merci d'avance.
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 20 Oct 2010, 15:12
par muse » 20 Oct 2010, 15:12
tu n'arrives pas a faire la question 1 ? meme pas la a ? c'est pourtant pas compliqué si tu arrives a afficher le graphe sur ta calculatrice ....
-
SteezyRider
- Membre Naturel
- Messages: 17
- Enregistré le: 29 Sep 2010, 15:28
-
 par SteezyRider » 20 Oct 2010, 18:10
par SteezyRider » 20 Oct 2010, 18:10
Je ne comprends pas. Pour la 1, il faut simplement faire avec la calculette, sans démontrer ?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 20 Oct 2010, 19:44
par Sa Majesté » 20 Oct 2010, 19:44
Oui
D'ailleurs on ne te demande pas de démontrer mais de conjecturer
-
SteezyRider
- Membre Naturel
- Messages: 17
- Enregistré le: 29 Sep 2010, 15:28
-
 par SteezyRider » 24 Oct 2010, 14:28
par SteezyRider » 24 Oct 2010, 14:28
Merci beaucoup !
-
SteezyRider
- Membre Naturel
- Messages: 17
- Enregistré le: 29 Sep 2010, 15:28
-
 par SteezyRider » 24 Oct 2010, 14:48
par SteezyRider » 24 Oct 2010, 14:48
Je bloque maintenant à l'exercice 3, je ne sais pas comment commencer, pouvez vous m'aider un petit peu ?
Merci d'avance.
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 24 Oct 2010, 14:53
par Jimm15 » 24 Oct 2010, 14:53
SteezyRider a écrit:Je bloque maintenant à l'exercice 3, je ne sais pas comment commencer, pouvez vous m'aider un petit peu ?
Merci d'avance.
Salut,
Il faut raisonner avec le centre de gravité

de

et le centre de gravité
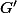
de
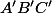
.
Tu peux commencer par dire que,

étant le centre de gravité du triangle

, on a :
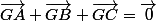
Autrement dit,

est lisobarycentre de

,

et

.
-
SteezyRider
- Membre Naturel
- Messages: 17
- Enregistré le: 29 Sep 2010, 15:28
-
 par SteezyRider » 24 Oct 2010, 15:26
par SteezyRider » 24 Oct 2010, 15:26
Jimm15 a écrit:Salut,
Il faut raisonner avec le centre de gravité

de

et le centre de gravité
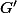
de
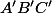
.
Tu peux commencer par dire que,

étant le centre de gravité du triangle

, on a :
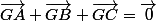
Autrement dit,

est lisobarycentre de

,

et

.
Oui, mais dois-je utiliser la propriété fondamentale ou une relation de vecteur ?
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 24 Oct 2010, 15:29
par Jimm15 » 24 Oct 2010, 15:29
SteezyRider a écrit:Oui, mais dois-je utiliser la propriété fondamentale ou une relation de vecteur ?
Tu peux me rappeler cette propriété fondamentale ?
-
SteezyRider
- Membre Naturel
- Messages: 17
- Enregistré le: 29 Sep 2010, 15:28
-
 par SteezyRider » 24 Oct 2010, 15:41
par SteezyRider » 24 Oct 2010, 15:41
a b et c 3 nombres tels que a+b+c =/= 0
Pour tout point M du plan :
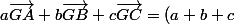\vec{MG})
D'autre part, une autre propriété stipule que, dans un triangle, avec mon énoncé, on aurait :
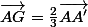
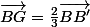
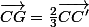
-
SteezyRider
- Membre Naturel
- Messages: 17
- Enregistré le: 29 Sep 2010, 15:28
-
 par SteezyRider » 24 Oct 2010, 16:10
par SteezyRider » 24 Oct 2010, 16:10
J'ai peut-être trouvé quelque chose, pouvez vous me dire si c'est bon ?
Avec la propriété fondamentale, pour le même point M du plan, on a
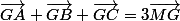
et
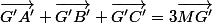
Si l'on choisit E l'ensemble des points pour lesquels
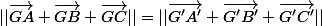
donc
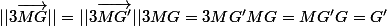
Est-ce que cela pourrait marcher ?
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 24 Oct 2010, 16:16
par Jimm15 » 24 Oct 2010, 16:16
Tu peux utiliser la seconde propriété et « arranger » la relation que tu obtiens afin davoir
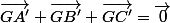
.
Rappel :  . Cest valable pour autant de vecteurs que lon veut.
. Cest valable pour autant de vecteurs que lon veut.
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 24 Oct 2010, 16:20
par Jimm15 » 24 Oct 2010, 16:20
SteezyRider a écrit:J'ai peut-être trouvé quelque chose, pouvez vous me dire si c'est bon ?
Avec la propriété fondamentale, pour le même point M du plan, on a
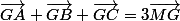
et
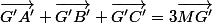 [I]Si l'on choisit
[I]Si l'on choisit[/I] E l'ensemble des points pour lesquels
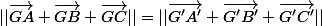 ==> Donc ce nest pas une égalité vraie. Cest une équation !!
==> Donc ce nest pas une égalité vraie. Cest une équation !!donc
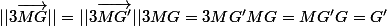 ==> Ah bon ?? :doh:
==> Ah bon ?? :doh: Est-ce que cela pourrait marcher ?
Il y a des choses à revoir.
-
SteezyRider
- Membre Naturel
- Messages: 17
- Enregistré le: 29 Sep 2010, 15:28
-
 par SteezyRider » 24 Oct 2010, 17:59
par SteezyRider » 24 Oct 2010, 17:59
Ahahahahahah désolé, j'me disais bien aussi que c'était bizarre, au bout de 3h de DM de maths j'commence à délirer un peu !
Merci, j'pense que maintenant je vais y arriver, grâce à ta réponse.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités

