Equation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Stephan2iie
- Membre Naturel
- Messages: 13
- Enregistré le: 08 Sep 2009, 15:21
-
 par Stephan2iie » 08 Sep 2009, 19:29
par Stephan2iie » 08 Sep 2009, 19:29
Bonjour. Quelqu'un pourrez t'il m'aidez à résoudre cette équation ?
Je n'y arrive vraiment pas. Merci
3) 2(2x-1)²(2x+1)= (4x²-1)²
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 08 Sep 2009, 19:31
par girdav » 08 Sep 2009, 19:31
Bonjour.
Factorise le membre de droite grâce à
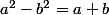\(a-b\))
.
-
Stephan2iie
- Membre Naturel
- Messages: 13
- Enregistré le: 08 Sep 2009, 15:21
-
 par Stephan2iie » 08 Sep 2009, 19:46
par Stephan2iie » 08 Sep 2009, 19:46
Ok, aprés j'ai fais:
2(2x-1)²(2x+1)-(2x+1)(2x+1)(2x-1)²= 0
Mais aprés je ne vois pas comment faire.
-
Aurelien08
- Membre Naturel
- Messages: 36
- Enregistré le: 05 Nov 2008, 00:00
-
 par Aurelien08 » 08 Sep 2009, 19:49
par Aurelien08 » 08 Sep 2009, 19:49
Bonjour

^{2}(2x+1)=(4x^{2}-1)^{2}}\\<br />\text{2(2x-1)(4x^{2}-1)=(4x^{2}-1)^{2}}\\<br />\text{Ensuite tu dois savoir que ka-kb=k(a-b)})
Si tu souhaite un peut plus de détaillle n'hesite pas

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 08 Sep 2009, 20:11
par Ericovitchi » 08 Sep 2009, 20:11
il suffit de mettre (2x+1)(2x-1)² en facteur
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 08 Sep 2009, 20:13
par oscar » 08 Sep 2009, 20:13
Bonsoir
Il y a deux facteurs communs
-
Stephan2iie
- Membre Naturel
- Messages: 13
- Enregistré le: 08 Sep 2009, 15:21
-
 par Stephan2iie » 08 Sep 2009, 20:15
par Stephan2iie » 08 Sep 2009, 20:15
Oui mais je ne vois pas commun faire la suite même si les 2 facteurs communs sont: (2x-1)² et (2x+1).

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 08 Sep 2009, 21:22
par Ericovitchi » 08 Sep 2009, 21:22
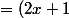(2x-1)^2[2-(2x+1)]=(2x+1)(2x-1)^2(1-2x)=0)
Et donc pour que ça soit égal à zéro, il suffit qu'un des facteurs soit nul et donc x= ... ; ... ; ...
-
Stephan2iie
- Membre Naturel
- Messages: 13
- Enregistré le: 08 Sep 2009, 15:21
-
 par Stephan2iie » 09 Sep 2009, 11:39
par Stephan2iie » 09 Sep 2009, 11:39
Je trouve comme solution -1/2 et 1/2 .
C'est ça ?
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 09 Sep 2009, 12:07
par Timothé Lefebvre » 09 Sep 2009, 12:07
Salut :)
Erico n'est pas là alors je me permets de te répondre à sa place. En me basant sur l'équation de son dernier post je peux dire qu'il te manque une solution (il précise bien qu'il y en a 3 en plus) : laquelle d'après toi ?
-
Stephan2iie
- Membre Naturel
- Messages: 13
- Enregistré le: 08 Sep 2009, 15:21
-
 par Stephan2iie » 10 Sep 2009, 17:46
par Stephan2iie » 10 Sep 2009, 17:46
En fait je trouve -1/2 ; 1/2 ; et encore -1/2.
C'est ca ou pas ?
;)
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 10 Sep 2009, 17:49
par Timothé Lefebvre » 10 Sep 2009, 17:49
Oui c'est ça lol, je t'ai dit qu'il y en avait 3 mais en fait il y en a 2 égales donc c'est bon :) Désolé !
-
Stephan2iie
- Membre Naturel
- Messages: 13
- Enregistré le: 08 Sep 2009, 15:21
-
 par Stephan2iie » 10 Sep 2009, 17:53
par Stephan2iie » 10 Sep 2009, 17:53
Ok merci :D
J'ai enfin trouvé ^^
Bonne soirée à toi

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 10 Sep 2009, 17:53
par Ericovitchi » 10 Sep 2009, 17:53
C'est ma faute

, j'aurais pu voir que
(2x-1)^2[2-(2x+1)]=(2x+1)(2x-1)^2(1-2x)= -(2x+1)(2x-1)^3)
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 10 Sep 2009, 17:54
par Timothé Lefebvre » 10 Sep 2009, 17:54
Lol merci bien, bonne soirée à toi aussi !
:salut:
EDIT Erico : j'aurais pu le voir aussi :ptdr:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
