Système à paramètre

[Tibwoo]

Bonjour a toi aussi,

Je suis coincé et à part résoudre ce système ( facile ) je n'arrive pas à répondre à ce qui est demandé pouvez me donner un coup de pouce :++: ?

Soit a un réel fixé
Pour tout on définit le système paramétré par et d'inconnues ( x,y,z )


on donne différentes valuer pour .
Par exemple = 1
MQ l'ensemble des solutions est la droite dirrigée par
(1,1,1)

[prody-G]

Je suis coincé et à part résoudre ce système ( facile ) je n'arrive pas à répondre à ce qui est demandé pouvez me donner un coup de pouce :++: ?

Soit a un réel fixé
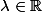
Pour tout on définit le système paramétré par et d'inconnues ( x,y,z )


on donne différentes valuer pour .
Par exemple = 1
MQ l'ensemble des solutions est la droite dirrigée par
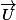
(1,1,1)

En fait résoudre le système c'est exactement répondre à la question :we:

Si tu as résolu le système c'est que tu as trouvé les triplets (x,y,z) qui vérifient ce système d'équation. Il faut en fait voir l'ensemble de ces solutions comme les points d'une droite.

C'est quoi que tu as comme solutions ?

[Tibwoo]

j'obtient sauf erreur de calcul x=y=z=0
Mais il est evident de voir que 1 est solution pour \lambda = 1

[amor]

salut est ce que vous avez utiliser la methode de Crammer en algebre lineaire?(en utilisant la matrice)

[prody-G]

j'obtient sauf erreur de calcul x=y=z=0
Mais il est evident de voir que 1 est solution pour \lambda = 1

hmm ce n'est pas correct de dire que 1 est solution, en fait les solutions sont des triplets (x,y,z). Par exemple (1,1,1) est solution puisque c'est ça que tu dois montrer. Par homogénéité, les (m,m,m) avec m réel sont solutions. Essaie de résoudre ce système avec le pivot de gauss par exemple.

[Tibwoo]

quand je disai 1 est solution je pensai au triplet (1,1,1 ) excuse moi pour le manque de rigueur.
J'ai déja résolu ce système par pivot de Gauss.c'est la que j'ai obtenu (0,0,0)
Un ami m'a dit qu'il fallait faire des opération sur les lignes jusqu'a trouver quelque chose de la forme .a*(mx+my+mz) = 0
Pensez-vous que sa soit une bonne idée ?

[prody-G]

quand je disai 1 est solution je pensai au triplet (1,1,1 ) excuse moi pour le manque de rigueur.
J'ai déja résolu ce système par pivot de Gauss.c'est la que j'ai obtenu (0,0,0)
Un ami m'a dit qu'il fallait faire des opération sur les lignes jusqu'a trouver quelque chose de la forme .a*(mx+my+mz) = 0
Pensez-vous que sa soit une bonne idée ?

Je sais pas si ça va t'avancer à quelque chose, mais en fait y a plus simple :
Si tu numérotes les lignes L1, L2 et L3, en faisant l'opération
L2+aL1 tu obtiens un truc intéressant.
De même avec L1+aL2, ça devrait te donner le résultat =D

[Tibwoo]

Merci beaucoup =D