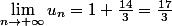bonjour, j'ai fait un exercice et j'aimerais savoir si ce que j'ai fait est juste, merci d'avance.
Soit
)
la suite définie sur

par :
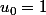
,
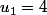
et
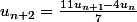
.
1°) Soit
)
la suite définie sur
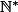
par
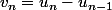
.
Démontrer que
)
est une suite géométrique dont on précisera le premier terme et la raison.
2°) Exprimer

en fonction de

et montrer que la suite
)
est strictement croissante.
3°) On pose :
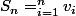
; calculer

de deux façon différentes et en déduire l'expression de

en fonction de

.
Montrer que
)
converge vers une limite que l'on précisera.
Voilà ce que j'aurais fait :
1°)
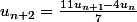
équivaut à
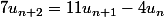
.
Par suite :
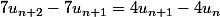
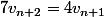
donc
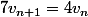
et par conséquent
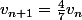
.
Donc
)
est suite géométrique de raison
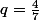
et de premier terme
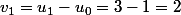
.
2°)
)
est une suite géométrique donc
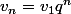
.
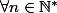
:
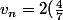^n)
.
Or

donc
^n>0)
et par conséquent
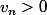
.
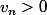
équivaut à

donc
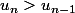
.
Donc (u_n) est strictement croissante.
3°)
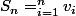
donc :
*
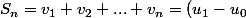+(u_2-u_1)+...+(u_n-u_{n-1})=u_n-u_0=u_n-1)
*
^{n+1}}{1-\frac{4}{7}}=\frac{14}{3}(1-(\frac{4}{7})^{n+1}))
Par suite, il vient :
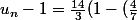^{n+1}))
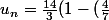^{n+1})+1)
.
Or

donc