Tu sais ce que c'est un changement de variables ?
Par exemple ici, le dénominateur

nous embête, on pose alors
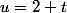
! Ce n'est pas plus compliqué que cela ! Ca veut dire que dans ton intégrale, tu remplaces tous les t par

. Attention à bien changer les bornes aussi !
Un exemple simple :
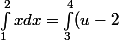 du)
Ici, j'ai fait le changement de variables

. Evidemment, il ne sert à rien dans ce cas, car on sait calculer la première intégrale sans changement de variables, mais c'est pour te montrer comment on fait. La chose qu'on oublie souvent, c'est de changer les bornes. Tu comprends que si x varie entre

et

, alors pour que les deux intégrales soient égales, il faut que
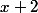
varie entre

et

, oui ?
En fait, quand tu dois faire un changement de variables dans une intégrale, la question que tu dois te poser c'est "qu'est-ce qui m'embête ?". Dans ton cas, c'est le dénominateur en 2+t (on aurait aimé avoir du t, non ?)
N'hésite pas à poser des questions !