Suite trigonometrique

[ninis0201]

Bonjour à tous, j'ai un exercice et je rencontre quelques problèmes :

On se propose de démontrer que les suites (un) et (vn) définie sur N, par :

un=cos n et vn=sin n
n'admettent pas de limites

1) On suppose que la suite (un) converge vers un réel L,
Démontrer que pour tout n, u2n= 2un²-1 ( Ici , c'est bon )
En déduire que L= 2L²-1, je ne comprends pas le rapport ... ça doit être tout simple mais je ne trouve pas.

2)Démontrer que pour tout n>1 : un+1+un-1 = 2uncos1
Ici , je ne comprend pas du tout !

Si vous pouviez m'aider

Cordialement.

[Maks]

Bonjour.
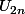
Regarde. Si a pour limite quand tend vers , alors quelle est la limite de ? Et celle de ?

[ninis0201]

Euh, je pense que c'est L , intuitivement ...

[Maks]

Regarde, ça va peut-être t'aider.

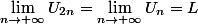
, ça, tu l'as. C'est bien.

Tu fais pareil avec l'autre expression :

?

Ca te parle plus ?

[ninis0201]

Ah oui =D

donc, si j'ai bien compris , lim 2un²-1 = 2L²-1 !
Et donc là c'est prouvé !

[Maks]

Oui. Essaie la suite.

[ninis0201]

Alors,

un+1 + un-1= cosn+1 + cosn-1
= 2cos n puisque 1-1=0
Mais alors , j'arrive à 2un mais je n'ai pas de cos1 ...


A moins qu'il faille prendre
un+1 + un-1 = cos(n+1) + (cos n-1)


ça ne doit pas être bon ! :hum:

[Ericovitchi]

tu n'étais pas en train de nous dire que cos(a+b)=cos(a)+cos(b) j'espère :hum:

il faut connaître ses formules :
cos(a+b) = cos(a)cos(b) -sin (a)sin(b)
Appliqué à cos(n+1)+cos(n-1) ça donne ?

[ninis0201]

Ah d'accord,
Il faut donc prendre cos (a+b) avec a = n et b =1
et sin (a+b) avec a = n et b=1

Ca ferait ;
(cosn cos1 - sin n sin 1) + ( cos n cos 1 + sin n sin1)
ainsi
un+1 + un-1 = cosn cos1 + cosn cos 1
= cos1 * 2cosn
= 2un cos 1

Pas sure ... :doh:

[Ericovitchi]

Pourquoi pas sûre ? c'est bien ça que l'on t'as demandé de trouver, non ?

[ninis0201]

Oui c'était ça , mais je ne savais pas si c'était bien prouvé !

Merci beaucoup pour votre aide :)