Equation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
zag
- Messages: 8
- Enregistré le: 28 Sep 2007, 17:46
-
 par zag » 14 Mai 2009, 16:31
par zag » 14 Mai 2009, 16:31
Bonsoir... dsl
Bonjour à toi aussi !!Je cherche à résoudre l'équation:
2^(n-1)=n+1 soit en posant m=n+1 et donc m-2=n-1 il vient:
2^(m-2)=m soit encore:
2^m=4m
Il va de soit que m=4 est une solution mais comment le démontrer? Passer en log ne rend pas vraiment plus limpide cette équation qui s'écrit alors:
mln2=2ln2+lnm
D'autre part si n est un réel, il existe graphiquement une autre solution que m=4 (soit n=3), puisque la fonction 2^m a deux intersections avec la fonction linéaire 4m.
En gros comment résoudre cette équation

. Merci
-
zag
- Messages: 8
- Enregistré le: 28 Sep 2007, 17:46
-
 par zag » 14 Mai 2009, 17:24
par zag » 14 Mai 2009, 17:24
Oui pardon bonsoir, j'étais trop dans mon truc désolé...
En ce qui concerne mon problème, puisqu'il y a deux solutions, il y a sûrement une équation du deuxième degré la dessous, mais laquelle ?
-
zag
- Messages: 8
- Enregistré le: 28 Sep 2007, 17:46
-
 par zag » 15 Mai 2009, 10:53
par zag » 15 Mai 2009, 10:53
Re bonjour
Personne à une idée?
Mci
-
Cheche
- Membre Rationnel
- Messages: 650
- Enregistré le: 17 Avr 2009, 19:25
-
 par Cheche » 15 Mai 2009, 11:47
par Cheche » 15 Mai 2009, 11:47
Salut,
Je pense que cette question peut se résoudre de manière analytique (utilise les chapitres d'analyse : les études de fonction ...)
Pour tout n |N, 2^(n-1)=n+1
<=> Pour tout m |N*, 2^m =4 * m
<=> Pour tout m |N*, m* ln2=ln(4*m)
<=> Pour tout m |N*, ln2 = ln(4*m) / m
Étude de la fonction : f(x) = ln(4*x) / x
Ensuite tu calcules la dérivée, tu fais un tableau de variation. Et tu cherches les solutions de l'équation f(x) = ln 2.
-
zag
- Messages: 8
- Enregistré le: 28 Sep 2007, 17:46
-
 par zag » 15 Mai 2009, 12:21
par zag » 15 Mai 2009, 12:21
Merci, je le voyais comma ça aussi, mais à force d'enseigner dans le secondaire, on en oublie les bases, ou en tout cas on perd confiance! Bon week end.
 par busard_des_roseaux » 15 Mai 2009, 13:28
par busard_des_roseaux » 15 Mai 2009, 13:28
bonjour,
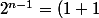^{n-1} \geq 1+(n-1)+\frac{(n-1)(n-2)}{2})
pour n>1 car ce sont les trois premiers termes du développement
du binôme (sorte d'
inégalité de Bernoulli )
mézalor,
+\frac{(n-1)(n-2)}{2}> n+1)
si n>3
d'où l'unique solution n=3
-
zag
- Messages: 8
- Enregistré le: 28 Sep 2007, 17:46
-
 par zag » 17 Mai 2009, 10:25
par zag » 17 Mai 2009, 10:25
Merci je vais regarder ça.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
