Fonctions carré

par **baptiste79** » 08 Mai 2009, 17:31

Bonjour a tous,

J'ai un petit exercice sur les fontions ou je bloque et j'ai besoin de votre aide !

f est la fonction définie sur R par : f(x) = x² - 6x +6

1°: Montrer que pour tout x appartenant à R, f(x) = (x-3)² -3

Que dois je faire ?

Merci

par **le_fabien** » 08 Mai 2009, 17:32

Bonjour,
tu as juste a developper la deuxième forme que l'on te donne et le tour est joué.

par **baptiste79** » 08 Mai 2009, 17:47

Je mets ca :

f(x) = (x-3)² -3
= x²-6x+9-3
=x²-6x-6

Comment je conclue je mets pas = f(x) ou autre chose ?

par **le_fabien** » 08 Mai 2009, 17:51

baptiste79 a écrit:Je mets ca :

(x-3)² -3
= x²-6x+9-3
=x²-6x-6=f(x)

Comment je conclue je mets pas = f(x) ou autre chose ?

Comme cela plutôt. :zen:

par **baptiste79** » 08 Mai 2009, 17:55

ca est une contraction de cela ! :id:

Et pour ma question c'est bon ?

par **le_fabien** » 08 Mai 2009, 18:02

Tu ne mets que cela :
(x-3)² -3
= x²-6x+9-3
=x²-6x-6=f(x)

par **baptiste79** » 08 Mai 2009, 18:03

ok merci beaucoup

Et apres je dois étudier le sens de variation sur quel intervalle dois-je travailler ?

par **le_fabien** » 08 Mai 2009, 18:05

Sur ]-inf;3] et sur [3;+inf[

par **baptiste79** » 08 Mai 2009, 18:08

C'est bien ce que je pensais mais en réalité je voulais savoir si il fallait justifier cet intervalle ?

par **le_fabien** » 08 Mai 2009, 18:09

Non pas spécialement, l'étude de variation le justifiera.

par **baptiste79** » 08 Mai 2009, 18:14

MERCI POUR TOUS T'ES SUPER !!! :we:

par **supermatheux** » 08 Mai 2009, 19:31

le_fabien a écrit:Tu ne mets que cela :
(x-3)² -3
= x²-6x+9-3
=x²-6x-6=f(x)

heuu... pour moi x²-6x+9-3=x²-6x+6 et non x²-6x-6 ou je me trompe??? :hein:

par **le_fabien** » 08 Mai 2009, 19:42

supermatheux a écrit:heuu... pour moi x²-6x+9-3=x²-6x+6 et non x²-6x-6 ou je me trompe??? :hein:

Oui exactement , il a pas fait attention... :hein:

par **nice** » 08 Mai 2009, 19:51

baptiste79 a écrit:Bonjour a tous,

J'ai un petit exercice sur les fontions ou je bloque et j'ai besoin de votre aide !

f est la fonction définie sur R par : f(x) = x² - 6x +6

1°: Montrer que pour tout x appartenant à R, f(x) = (x-3)² -3

Que dois je faire ?

Merci

Salut à tous

à mon avis il serait mieux de faire
f(x)= x²-6x+6= (x²-3*2*x+3²)-9+6= (x-3)²-3

En fait la forme canonique qui permet de passer de x²-6x+6 à (x-3)² -3

par **le_fabien** » 08 Mai 2009, 19:56

nice a écrit:Salut à tous

à mon avis il serait mieux de faire
f(x)= x²-6x+6= (x²-3*2*x+3²)-9+6= (x-3)²-3

En fait la forme canonique qui permet de passer de x²-6x+6 à (x-3)² -3

Cela dépend si il est en seconde ou pas, la forme canonique ne se voit généralement qu'en première.

par **nice** » 08 Mai 2009, 20:31

le_fabien a écrit:Cela dépend si il est en seconde ou pas, la forme canonique ne se voit généralement qu'en première.

peut etre puisque les programmes différent légèrement d'un pays à un autre
Sinon moi j'ai vu la forme canonique en classe de seconde.
Vu le sujet c'est le procédé à utiliser car c'est une démonstration et non une justification

par **SasuKe Uchiwara** » 08 Mai 2009, 20:32

x²-6x+6 à (x-3)² -3
Facile !

par **fibonacci** » 09 Mai 2009, 04:29

Bonjour;

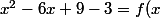là ne s'arrête pas le boulot.

Pour l'étude de f(x)

sg de f(x)?

]-

sg de f(x)?

par **oscar** » 09 Mai 2009, 08:52

Bjr

Les racines de (x-3)² -3 = ( x-3-v3)( x-3+V3)=A
sont x-3+v3 = 0=> x =3-v3 et x-3-v3=0=> x= 3+v3

Tableau
x..............3-v3..............3+v3......
A+++++++0-----------------0++++++++
Tu as ainsi les signes de A suivant les valeurs de x

u

Fonctions carré

Fonctions carré

Qui est en ligne