Sens de variation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
magnum
- Membre Relatif
- Messages: 149
- Enregistré le: 22 Avr 2007, 09:12
-
 par magnum » 26 Avr 2009, 09:39
par magnum » 26 Avr 2009, 09:39
Bonjour,
Je dispose de la fonction suivante définie sur R+
f(t)= sint/t si t >0
1 si t=0
Mq f est décroissante sur [0,1] et -1
J'ai essayé de dériver, je n'arrive pas à étudier le signe, j'ai aussi essayé f(a)-f(b) ça ne donne rien ...
Merci de votre aide !
-
magnum
- Membre Relatif
- Messages: 149
- Enregistré le: 22 Avr 2007, 09:12
-
 par magnum » 26 Avr 2009, 10:27
par magnum » 26 Avr 2009, 10:27
j'ai trouvé pour la seconde mais il me manque le sens de variation
si je calcule la dérivée, ça me donne 1/t² ( tcost - sint) je ne vois pas comment étudier le signe , en faisant f(a) - f(b) rien d'intéressant non plus.
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 26 Avr 2009, 10:35
par axiome » 26 Avr 2009, 10:35
Bonjour,
Essaie peut-être de calculer la dérivée seconde pour avoir les variations de la dérivée : avec un peu de chance, d'après les variations de la dérivée, tu pourras avoir son signe et du coup déduire les variations de

sur
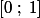
...
-
magnum
- Membre Relatif
- Messages: 149
- Enregistré le: 22 Avr 2007, 09:12
-
 par magnum » 26 Avr 2009, 10:43
par magnum » 26 Avr 2009, 10:43
OK je trouve que la dérivée seconde est négative, la dérivée première est décroissante mais je ne connait pas sa valeur en 0 pour conclure ! Je commence à douter que la dérivation soit la bonne méthode dans ce cas .
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 26 Avr 2009, 10:45
par axiome » 26 Avr 2009, 10:45
Tu dis que la dérivée première est décroissante.
Quelle est sa valeur en 1 ?
Je n'ai pas fait les calculs...
-
magnum
- Membre Relatif
- Messages: 149
- Enregistré le: 22 Avr 2007, 09:12
-
 par magnum » 26 Avr 2009, 10:50
par magnum » 26 Avr 2009, 10:50
sa valeur en 1 ne nous donnera rien , c'est sa valeur en 0 qui est intéressante sinon elle peut très bien changer de signe entre les 2. Notre objectif étant de démontrer qu'elle est toujours négative.
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 26 Avr 2009, 10:57
par axiome » 26 Avr 2009, 10:57
magnum a écrit:sa valeur en 1 ne nous donnera rien , c'est sa valeur en 0 qui est intéressante sinon elle peut très bien changer de signe entre les 2. Notre objectif étant de démontrer qu'elle est toujours négative.
Non,
C'est surtout sa valeur en 1 qui est intéressante.
Tu as montré que la dérivée première est strictement décroissante sur [0 ; 1].
Si jamais sa valeur en 1 est positive, cela veut dire que la dérivée première est positive. Et donc que la fonction est croissante sur [0 ; 1].
Si jamais la valeur en 1 de la dérivée première est négative, on ne pourra alors rien dire pour le signe de cette dérivée première...

-
magnum
- Membre Relatif
- Messages: 149
- Enregistré le: 22 Avr 2007, 09:12
-
 par magnum » 26 Avr 2009, 11:06
par magnum » 26 Avr 2009, 11:06
vu que l'on veut montrer que c'est décroissant c'est un peu mort ...
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 26 Avr 2009, 11:07
par axiome » 26 Avr 2009, 11:07
Désolé, autant pour moi, cette méthode ne marche pas, le but étant de démontrer que la fonction est décroissante.
J'avais mal lu le problème. J'avais lu : étudier les variations de f sans avoir vu qu'on était guidé, que la fonction devait être décroissante...
:marteau:
-
Cheche
- Membre Rationnel
- Messages: 650
- Enregistré le: 17 Avr 2009, 19:25
-
 par Cheche » 26 Avr 2009, 11:58
par Cheche » 26 Avr 2009, 11:58
Bonjour,
D'abord je voudrais commencer à dire de faire attention quand tu utilises les dérivées ... car on ne s'est pas toujours si les fonctions sont dérivables.
En effet, ta fonction est ici uniquement dérivable sur ]0;+infini[ (quotient de fonction dérivable, le dénominateur ne s'annulant pas).
Bref, c'était juste une petite remarque, car on oublie souvent les quantificateurs : (Pour tout x appartenant à ...)
Pour tout x appartenant à ]0;+infini[, f'(x) = 1/t² ( t*cost - sint)
Etude du signe de f' sur ]0;1] :
équivaut à l'étude du signe de t*cost - sint sur ]0;1]
Après calcul, tu remarques que t*cost - sint est négatif sur [0;1] donc sur ]0;1].
Problème résolu sur ]0;1]. Il ne reste plus qu'à régler le cas de 0.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités