Problème de vecteurs
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Breizhoo29
- Messages: 9
- Enregistré le: 25 Avr 2009, 18:19
-
 par Breizhoo29 » 25 Avr 2009, 18:36
par Breizhoo29 » 25 Avr 2009, 18:36
Bonjour à tous.
Je suis bloqué à mon devoir maison. voici le sujet:

On s'intéresse à la branche d'hyperbole et à ses asymptotes
et un point M appartient à celle-ci si OR x OS = k où k note une constante.
1°) En partant de OR x OS = OR' x OS ',
démontrer en utilisant Thalès que
MP x MQ = M' P x M' Q
2°) I est le milieu de [MM' ]
Justifier que MP . MQ = M'P . M'Q
et en déduire que IP^2=IQ^2
Quelle conclusion pour I, et pour les longueurs
MQ et M'Q ?
3°) Dans le cas de la tangente :
traduire les résultats précédents et démontrer que :
OP x OQ = constante
Conclure que l'aire de OPQ quand M varie
est constante en utilisant une bonne formule
pour l'aire
Les vecteurs sont en rouge

. Je suis bloqué à la question 2. Je vois pas du tout comment faire. J'ai essayé la relation de chasles mais rien n'y fait.
Pourriez-vous m'aider SV.
Merci d'avance


-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 25 Avr 2009, 19:18
par fatal_error » 25 Avr 2009, 19:18
salut,
pour la premiere question de la 2 utilise la relation
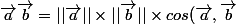)
la vie est une fête

-
Breizhoo29
- Messages: 9
- Enregistré le: 25 Avr 2009, 18:19
-
 par Breizhoo29 » 25 Avr 2009, 19:51
par Breizhoo29 » 25 Avr 2009, 19:51
Ah oui j'y avais pas pensé merci.
Mais ensuite, y a rien qui met en relation IP ou IQ :hum:

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 25 Avr 2009, 20:07
par fatal_error » 25 Avr 2009, 20:07
ben vu que M c'est un point quelconque, tu peux choisir en particulier de mettre M en I et M' en I
la vie est une fête


-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 25 Avr 2009, 20:30
par fatal_error » 25 Avr 2009, 20:30
pour IP et IQ, tu peux tenter de faire intervenir le point I lorsque tu exprimes les distances.
Jor MQ=IQ-MI par exemple.
si tu fais ca pour les quatre termes de legalité que tu as précédemment justifiée, ya moyen que ca simplifie bien et que tu trouves le resultat attendu
la vie est une fête

-
Breizhoo29
- Messages: 9
- Enregistré le: 25 Avr 2009, 18:19
-
 par Breizhoo29 » 25 Avr 2009, 21:48
par Breizhoo29 » 25 Avr 2009, 21:48
Je trouve (MI+IP).(IQ-MI) = (IP-IM').(IM'+IQ)
En sachant que MI= IM', pour les simplifier il faudrait que les échanges de cotés dans la fraction.
Comment on fait ca avec des produits scalaires?
-
freepol
- Membre Naturel
- Messages: 10
- Enregistré le: 26 Avr 2009, 08:29
-
 par freepol » 26 Avr 2009, 09:04
par freepol » 26 Avr 2009, 09:04
Eh bien c'est dans ses propriétés, au produit scalaire : tu peux le "distribuer" sur les sommes et les différences de vecteurs, c'est bien pour ça qu'il est si pratique...
Donc ton (IP-IM).(IM'+IQ) vaut, comme IM=-IM', (IP-IM)(IQ-IM)= IP.IQ-IM(IP+IQ)-IM.IM
-
Breizhoo29
- Messages: 9
- Enregistré le: 25 Avr 2009, 18:19
-
 par Breizhoo29 » 26 Avr 2009, 09:46
par Breizhoo29 » 26 Avr 2009, 09:46
Ouais mais si je fais ca des deux cotés je me retrouve, après simplification à:
IP.IQ = IP.IQ
simplifié a partir de ca:
(IP-IM).(IQ-IM) = (IP+IM).(IM+IQ)
IP.IQ-IM.(IP+IQ) +IM.IM = IM(IP+IQ) + IP.IQ + IM.IM
Mais si je reprend celle-ci:
(IP-IM).(IQ-IM) = (IP+IM).(IM+IQ)
Il faudrait que je puisse mettre les IP et les IQ ensembles on aurait alors:
(IP-IM).(IP+IM) = (IM+IQ).(IQ-IM)
Et avec les produits remarquables:
IP²-IM² = IQ² -IM²
IP² = IQ²
Mais est-ce possible?

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 26 Avr 2009, 10:09
par fatal_error » 26 Avr 2009, 10:09
re,
tout d'abord, la consigne impose/conseille (ca dépend du prof) de ne pas reprendre la formule avec le produit scalaire, car il est écrit "en déduire". Donc tu pars de ta formule précédente. (du moins c'est généralement ce raisonnement a appliquer).
Concernant le produit
(IP-IM).(IQ-IM) = (IP+IM).(IM+IQ) (IP-IM).(IP+IM) = (IM+IQ).(IQ-IM)
C'est bien sur pas la même chose. La tu sous entend que
(IQ-IM) = (IP+IM). Ou qqch dans le genre vu qu'on a des scalaires. Comme les vecteurs sont tous colinéaires, tu sous-entend (IQ-IM) = (IP+IM), ce qui tu pourras le vérifier est faux.
Donc faut bien partir de ta formule avec les distances. Tu as effectivement bien fait de remarquer IM=IM'.
la vie est une fête

-
Breizhoo29
- Messages: 9
- Enregistré le: 25 Avr 2009, 18:19
-
 par Breizhoo29 » 26 Avr 2009, 10:16
par Breizhoo29 » 26 Avr 2009, 10:16
fatal_error a écrit:re,
tout d'abord, la consigne impose/conseille (ca dépend du prof) de ne pas reprendre la formule avec le produit scalaire, car il est écrit "en déduire". Donc tu pars de ta formule précédente. (du moins c'est généralement ce raisonnement a appliquer).
C'est ce que j'ai fait, je suis parti du resultat précédent:
MP.MQ = M'P.M'Q
et j'ai utilisé Chasles ainsi que la relation IM = -IM'
d'où:
(IP-IM).(IQ-IM) = (IP+IM).(IM+IQ)
IP.IQ-IM.(IP+IQ) +IM.IM = IM(IP+IQ) + IP.IQ + IM.IM
IP.IQ = IP.IQ

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 26 Avr 2009, 10:20
par fatal_error » 26 Avr 2009, 10:20
t'as raté un paragraphe :
Donc faut bien partir de ta formule avec les distances
IM=-IM'???
Edit : autant pour moi, j'ai du mal a voir le rouge
la vie est une fête

-
Breizhoo29
- Messages: 9
- Enregistré le: 25 Avr 2009, 18:19
-
 par Breizhoo29 » 26 Avr 2009, 10:29
par Breizhoo29 » 26 Avr 2009, 10:29
Désolé, j'oubliais le rouge ;).
De toute façon, il n'y a que des vecteurs dans cette question

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 26 Avr 2009, 10:32
par fatal_error » 26 Avr 2009, 10:32
Du coup, c'est pas plus méchant :
il suffit de remarquer que

Donc une fois que t'as tout simplifié, tu passes en distances (vu que tes vecteurs sont colinéaires)
la vie est une fête


-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 26 Avr 2009, 10:37
par fatal_error » 26 Avr 2009, 10:37
IP.IQ-IM.(IP+IQ) +IM.IM = IM(IP+IQ) + IP.IQ + IM.IM
IP.IQ = IP.IQ
Cet enchainement est faux
tu simplifies -a=a en distant -a-a = 0 -2a=0 a=0
la vie est une fête

-
Breizhoo29
- Messages: 9
- Enregistré le: 25 Avr 2009, 18:19
-
 par Breizhoo29 » 26 Avr 2009, 10:46
par Breizhoo29 » 26 Avr 2009, 10:46
donc ca donnerai?
IP.IQ-IM.(IP+IQ) +IM.IM = IM(IP+IQ) + IP.IQ + IM.IM
IP.IQ-IM.(IP+IQ) +IM.IM - IM(IP+IQ) - IP.IQ - IM.IM = 0
-2IM.(IP+IQ) = 0
-2IM.IP = 2IM.IQ
-IP = IQ
d'où, IP² = IQ²
Woah, c'est bon alors. Génial, merci beaucoup fatal-error de m'avoir aidé, parce que je suis une bille en produit scalaires.^^
Merci aussi à Freepol :we:

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 26 Avr 2009, 10:51
par fatal_error » 26 Avr 2009, 10:51
avec plaisir :happy2:
la vie est une fête

-
Breizhoo29
- Messages: 9
- Enregistré le: 25 Avr 2009, 18:19
-
 par Breizhoo29 » 26 Avr 2009, 17:34
par Breizhoo29 » 26 Avr 2009, 17:34
Arf, je suis bloqué à la question suivante maintenant :mur:
Je vois pas comment, avec les résultats qu'on a, comment prouver, dans le cas de la tangente, OP x OQ = constante.
Pouvez vous, une nouvelle fois m'aider SVP :cry2:
-
Breizhoo29
- Messages: 9
- Enregistré le: 25 Avr 2009, 18:19
-
 par Breizhoo29 » 26 Avr 2009, 20:38
par Breizhoo29 » 26 Avr 2009, 20:38
UP s'il vous plait :triste:

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 28 Avr 2009, 12:39
par fatal_error » 28 Avr 2009, 12:39
re,
pour OPxOQ= cst :
Tu peux regarder du coté des aires. Sinon, faudrait un coup de thalès bien placé, pe, mais la j'ai pas le temps.
la vie est une fête

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités

