Intégrale de f''/f ??

[noucho]

Bonjour à tous,

une petite question vraiment en passant...
De façon formelle, pour toute fonction f dérivable et strictement positive, on sait intégrer


Qu'en est-il de
??

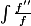
J'ai un peu cherché, pas trouvé, et conclu intérieurement que très vraisemblablement, aucune formule générale n'existe dans ce cas.
Êtes-vous d'accord ?

++,
Noucho

[noucho]

Merci, ta proposition est bien vue mais, d'après moi, ne marche pas...

Pour info, en dérivant 2 fois g=log(f), on peut voir que mon problème se ramène à celui de trouver une intégrale formelle pour (g')^2 (ou g peut être n'importe quelle fonction):
=??

Toujours pas d'amateurs ?

Merci de vos réponses,

à+,
Noucho

[busard_des_roseaux]

Merci de vos réponses,

effectivement, en transformant, on obtient les écritures

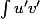
et/ou

qui n'ont pas des airs de différentielles exactes

[noucho]

qui n'ont pas des airs de différentielles exactes

eeh oui... ainsi va la vie

Par ailleurs, je suis curieux de l'expression "differentielle exacte" que tu utilises ? N'est-ce pas là un jargon normalement réservé aux formes différentielles à plusieurs variables, qui ne proviennent pas forcément de la différentiation d'une fonction ? (Alors qu'ici, (g')^2 *admet bien* une intégrale, même si on ne peut pas lui trouver d'expression anlytique).

Y aurait-il un parallèle entre le fait de pouvoir trouver une expression analytique à une intégrale, et des fonctions à plusieurs variables ? Ou bien as-tu utilisé le terme "différentielle exacte" comme un raccourci de langage, sur lequel je te prends la tête pour rien :we: ?

En tout cas !

@+,
Noucho

[busard_des_roseaux]

Par ailleurs, je suis curieux de l'expression "differentielle exacte" que tu utilises ? N'est-ce pas là un jargon normalement réservé aux formes différentielles à plusieurs variables, qui ne proviennent pas forcément de la différentiation d'une fonction ? (Alors qu'ici, (g')^2 *admet bien* une intégrale, même si on ne peut pas lui trouver d'expression analytique).

oui, d'accord avec ta remarque.

sinon, j'ai essayé de poser
où G serait la bijection réciproque d'une primitive de f. :hum: