Suite et récurrence
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Leo M
- Membre Naturel
- Messages: 28
- Enregistré le: 26 Oct 2008, 16:41
-
 par Leo M » 04 Fév 2009, 08:50
par Leo M » 04 Fév 2009, 08:50
Bonjour,
Alors j'ai ici:
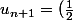(u_n+\frac{a}{u_n}))
Avec:

1- Montrer par récurrence que

pour tout n.
2- Montrer que la suite (

) est décroissante.
3- Etudier la convergence de (

).
J'ai tenté plusieurs fois la première question, mais sans succès. Je doute même qu'elle soit possible; d'ailleurs, ce qui est demandé est-il vrai? Sinon, je pense que je n'aurais pas de grandes difficultés à faire les 2 dernières questions si j'ai la réponse à la première.
Merci à vous!
-
phryte
- Membre Irrationnel
- Messages: 1406
- Enregistré le: 05 Juil 2008, 17:09
-
 par phryte » 04 Fév 2009, 09:07
par phryte » 04 Fév 2009, 09:07
Bonjour.
2Un+1=(Un^2+a)/Un
.....
-
Leo M
- Membre Naturel
- Messages: 28
- Enregistré le: 26 Oct 2008, 16:41
-
 par Leo M » 04 Fév 2009, 13:35
par Leo M » 04 Fév 2009, 13:35
Merci; j'ai réussi la récurrence!
Par contre, je trouve une "forme indéterminée" pour l'étude des variations (suite décroissante).
Une idée?
Merci.
-
Leo M
- Membre Naturel
- Messages: 28
- Enregistré le: 26 Oct 2008, 16:41
-
 par Leo M » 04 Fév 2009, 14:11
par Leo M » 04 Fév 2009, 14:11
Toujours rien?
Je n'arrive pas à justifier la décroissance de la suite
)
:/ .
-
phryte
- Membre Irrationnel
- Messages: 1406
- Enregistré le: 05 Juil 2008, 17:09
-
 par phryte » 04 Fév 2009, 14:29
par phryte » 04 Fév 2009, 14:29
Tu peux étudier la dérivée de : (en montrant qu'elle est <0 jusqu'à a )
 = \frac{1}{2}\left(x+\frac{a}{x}\right) ,)
-
Leo M
- Membre Naturel
- Messages: 28
- Enregistré le: 26 Oct 2008, 16:41
-
 par Leo M » 04 Fév 2009, 14:43
par Leo M » 04 Fév 2009, 14:43
D'accord d'accord, j'obtiens (x²-a)/(2x²). Mais je ne comprend pas votre démarche sur l'étude du signe de la dérivée :s .
-
phryte
- Membre Irrationnel
- Messages: 1406
- Enregistré le: 05 Juil 2008, 17:09
-
 par phryte » 04 Fév 2009, 14:46
par phryte » 04 Fév 2009, 14:46
La dérivée est <0 entre 0 et racine(a) donc la fonction décroit dans cette plage.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
