Bonjour,
Je dois appliquer Green Riemann pour calculer l'aire d'un triangle ABC à 3 coordonnées dans un plan.
Je ne vois pas du tout comment l'appliquer, j'ai regarder ce que disais le théorème, mais là ou je bloque c'est pour déterminer la forme différentielle.
Pourriez-vous me donner un coup de main.
Merci d'avance
Au revoir.
Aire triangle
10 messages
- Page 1 sur 1
Tu veux calculer

ou K représente la surface du triangle.
Nigthmare t'a fournit un bon champ de vecteurs (il y en a d'autres qui marchent aussi)

En faite le theorème de green -riemann dit que sous de bonne hypothese on a
dxdy=\Bigint_{\partial K} Pdx+Qdy)
Donc
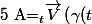 \right) \cdot \vec{\gamma'(t)}dt)
ou) est un parametrage
est un parametrage
(sauf erreur de ma part, mes souvenirs sont un peu loin ...)
ou K représente la surface du triangle.
Nigthmare t'a fournit un bon champ de vecteurs (il y en a d'autres qui marchent aussi)
En faite le theorème de green -riemann dit que sous de bonne hypothese on a
Donc
ou
(sauf erreur de ma part, mes souvenirs sont un peu loin ...)
Nightmare a écrit:En fait faire un paramétrage est idiot ici, on peut avoir directement une description du triangle par deux inégalités du type f(x) < y < g(x)
L'idée doit être de constater qu'on trouve effectivement la même chose quand on calcule la double integrale directement que lorsqu'on passe par green-riemann
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 103 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
