Calcul Intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pollop
- Messages: 3
- Enregistré le: 24 Déc 2008, 12:47
-
 par pollop » 24 Déc 2008, 12:53
par pollop » 24 Déc 2008, 12:53
Bonjour à tous

Je coince sur une intégrale depuis plus d'une heure et demi

Donc voilà, si quelqu'un sait me donner une petit coup de main se serait chouette

La voici :

J'ai commencé par intégré par partie mais ça coince quand même plus loin

u = arcsin x
u' = 1 / sqrt(1-x^2)
v' = 1 / x^2
v = -2 / x^3
On arrive donc à :

Ensuite je pose : x = sin t
Donc dx = cos t dt
On arrive à ceci :

Mais là je coince ...

Voilà, merci beaucoup pour votre aide.
Joyeux noël !
-
JJa
- Membre Relatif
- Messages: 254
- Enregistré le: 06 Mar 2008, 15:52
-
 par JJa » 24 Déc 2008, 13:09
par JJa » 24 Déc 2008, 13:09
Salut,
une façon de faire classique est de poser u=tg(t/2).
Mais on peut procéder autrement dans le cas présent :
1/sin(t)^3 = sin(t)/sin(t)^4
= -d(cos(t))/(1-cos²(t))²
-
pollop
- Messages: 3
- Enregistré le: 24 Déc 2008, 12:47
-
 par pollop » 24 Déc 2008, 13:23
par pollop » 24 Déc 2008, 13:23
Merci pour ta réponse.
Malheureusement je n'y arrive toujours pas :(
Même avec tg(t/2)
Et je n'ai pas bien compris ta seconde technique :/
-
izamane95
- Membre Rationnel
- Messages: 620
- Enregistré le: 31 Aoû 2006, 22:08
-
 par izamane95 » 24 Déc 2008, 13:40
par izamane95 » 24 Déc 2008, 13:40
bah oui ....regarde bien ta première intégration par partie est fausse...
si tu pose u = arcsin(x) ton v' c'est pas 1/x^2 que t'a marqué dans ton premier post
continue donc avec
)


.............
a part si tu t'es trompé dans ton premier post et que tu cherche à intégrer
/x^2)
-
pollop
- Messages: 3
- Enregistré le: 24 Déc 2008, 12:47
-
 par pollop » 24 Déc 2008, 13:50
par pollop » 24 Déc 2008, 13:50
Oups, en effet, je me suis trompé dans mon premier post !
Désolé, je viens de modifier !
-
izamane95
- Membre Rationnel
- Messages: 620
- Enregistré le: 31 Aoû 2006, 22:08
-
 par izamane95 » 24 Déc 2008, 14:04
par izamane95 » 24 Déc 2008, 14:04
ok imaginons que ce que t'a fait précedement est bon ...t'arrive à:
}{x^3})
+
^3}))
à partir de là tu pose
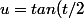)
donc t =2arctan(u) et

=\frac{2u}{1+u^2})
on a donc
^3}))
=
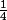
^2)
...et je pense pas que ça te posera problème aprés.. tu developpe et puis c'est fini
 par busard_des_roseaux » 24 Déc 2008, 16:00
par busard_des_roseaux » 24 Déc 2008, 16:00
pollop a écrit:J'ai commencé par intégré par partie mais ça coince quand même plus loin

u = arcsin x
u' = 1 / sqrt(1-x^2)
v' = 1 / x^2
v = -2 / x^3
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités



