Les suites

[emilie78]

bonjour j'ai quelques petits problèmes pour faire un exercice

un pays en voie de développement comptait en l'an 2000 trois millions d'enfants d'age compris entre 6 et 11ans. seul 700 000 d'entre eux étaient scolarisés.
on comparera la population d'age scolaire c'est a dire le nombre des enfants dont l'age est compris entre 6 et 11 ans et la population scolarisée, c'est à dire le nombre d'enfants qui sont inscrit dans une école.
la population d'age scolaire augmente de 2% par n at la population scolarisé de 150000 par an.

1) quel est le pourcentage de population dans ce pays en 2000?
2) on note p indice n la pop d'age scolarisé en 2000+n et s indice n la population scolarisée cette meme année.
a) quelles sont les valeurs de p indice 0 et S indice 0?
b) exprime le terme p indice n+1 en fonction de p indice n. en déduire l'expression de p indice n.
c) montrer que la suite s indice n est une suite arythmétique. en déduire l'expression de S indice n en fonction de n.
d) calculer le pourcentage de la population scolarisée en 2005
3) on note u indice n l'augentation par rapport à l'année précédente du nombre d'enfant d'age scolaire constatée l'année (2000+n) on a donc pour tt entier naturel n non nul, u indice n =p indice n - p indice (n-1).
a) calculer les termes u1 et u2
b) exprimer le terme général u indice n en fonction de n
c) calculer la somme de u1+u2+...+un en fonction de n. retrouver le nombre d'age scolaire prévu en 2005

Merciii de votre aide, je ne comprend riennnn!!!

[Luc]

Salut,

Déja, l'essentiel est de bien lire l'énoncé et d'en extraire les informations:


age scolaire : age compris entre 6 et 11 ans
en l'an 2000, trois millions d'enfants d'age compris entre 6 et 11ans
en l'an 2000, 700 000 d'entre eux étaient scolarisés
la population d'age scolaire augmente de 2% par an
la population d'enfants scolarisés augmente de 150000 par an

C'est tout ce dont tu as besoin pour résoudre l'exercice.
Quel est le but de l'exercice? De comparer population d'âge scolaire et population scolarisée. L'une est une suite géométrique, l'autre une suite arithmétique. Quelles sont leurs raisons respectives? Quelles sont les premiers termes?

=> Quelle est la définition d'une suite arithmétique ?
=> Quelle est la définition d'une suite géométrique?


1) quel est le pourcentage de population dans ce pays en 2000?

Cette question ne veut rien dire... Je suppose qu'on demande le pourcentage d'enfants d'âge scolaire qui sont scolarisés.

Essaye de dire précisément ce que tu ne comprends pas, je pourrai t'apprendre à faire l'exercice au lieu de le faire à ta place :id:

[Mathusalem]

bonjour j'ai quelques petits problèmes pour faire un exercice

un pays en voie de développement comptait en l'an 2000 trois millions d'enfants d'age compris entre 6 et 11ans. seul 700 000 d'entre eux étaient scolarisés.
on comparera la population d'age scolaire c'est a dire le nombre des enfants dont l'age est compris entre 6 et 11 ans et la population scolarisée, c'est à dire le nombre d'enfants qui sont inscrit dans une école.
la population d'age scolaire augmente de 2% par n at la population scolarisé de 150000 par an.

1) quel est le pourcentage de population dans ce pays en 2000?
2) on note p indice n la pop d'age scolarisé en 2000+n et s indice n la population scolarisée cette meme année.
a) quelles sont les valeurs de p indice 0 et S indice 0?
b) exprime le terme p indice n+1 en fonction de p indice n. en déduire l'expression de p indice n.
c) montrer que la suite s indice n est une suite arythmétique. en déduire l'expression de S indice n en fonction de n.
d) calculer le pourcentage de la population scolarisée en 2005
3) on note u indice n l'augentation par rapport à l'année précédente du nombre d'enfant d'age scolaire constatée l'année (2000+n) on a donc pour tt entier naturel n non nul, u indice n =p indice n - p indice (n-1).
a) calculer les termes u1 et u2
b) exprimer le terme général u indice n en fonction de n
c) calculer la somme de u1+u2+...+un en fonction de n. retrouver le nombre d'age scolaire prévu en 2005

Merciii de votre aide, je ne comprend riennnn!!!

Dire que tu ne comprends rien n'absout en rien le fait que tu n'as pas reflechi suffisamment au probleme. Il n'y a pas de telle chose que de ne rien comprendre.

On te donne des informations
Pour l'annee 2000 : Pop (6-11) = 3'000'000 ; Pop (6-11 Scolarise) = 700'000

Chaque annee, Pop (6-11) = 3'000'000 augmente de 2%
Chaque anne, Pop(6-11 Scolarise) = 700'000 augmente de 150'000

1) J'imagine qu'ils veulent le pourcentage de scolarises. Sinon il te manque des infos. Pour ceci, c'est Nb Enfants scolarises / Nb Enfants
= 700'000/3'000'000 = 7/30 = environ 23 %

2) On te dit de noter maintenant, pour le temps passant, la population au fil du temps comme pour les 3'000'000 d'enfants de depart, et pour les 700'000 de depart

L'indice n veut dire ceci : Nombres d'annees apres 2000

Par consequent, pour la 2a) Quel est le nombre d'age scolaire 0 annees apres 2000 ( donc en 2000 ) ; Quel est le nombre d'enfants scolarises 0 annes apres 2000 (donc en 2000 )
Tu devrais pouvoir repondre

2b) Tu as Selon les valeurs du texte, tu sais que = 2% de plus que l'annee precedente.
Donc, en general, si a une certaine annee, tu as x de population combien auras tu de population l'annee suivante ? ? ou x est la population a l'annee n . Tu peux donc aussi ecrire = Un certain facteur *
Je te laisse trouver ce facteur bien precis, a savoir qu'il doit symboliser une croissance de 2%. En trouvant ce facteur, et sachant la valeur de tu devrais trouver l'expression general de pour ce probleme

2C) Meme procede, sauf qu'il faut te rendre compte que ce n'est pas comme pour ou c'est un certain facteur *
Mais c'est une Addition d'enfants par annee.
Par consequent = Un certain nombre * n +

3) Tout as tout ce qu'il faut dans l'explication precedente et dans ton cours pour faire mumuse avec les expressions et t'en sortir pour la 3a 3b et 3c

Bonne chance

[emilie78]

enfaite j'ai déjà commencé mais mes résultats son biZarre.

pour la 1) (700000*3000000)/100= 23.33%

2) je crois qu'il faut appliqué p(n)= uo+(n*a)
mais je sais pas c'est quoi les valeurs et c'est de meme pour sn et le reste de l'exercie

[Luc]

enfaite j'ai déjà commencé mais mes résultats son biZarre.

pour la 1) (700000*3000000)/100= 23.33%

2) je crois qu'il faut appliqué p(n)= uo+(n*a)
mais je sais pas c'est quoi les valeurs et c'est de meme pour sn et le reste de l'exercie

Oui, la c'est p(n) = p(0) + n*a, mais

que vaut p(0) ? (donné dans l'énoncé, c'est la population d'age scolarisé en 2000).
que vaut a? (donné dans l'énoncé, c'est l'augmentation de cette population en un an).

Bon courage,

Luc

[emilie78]

donc p(n)= 70000+(n*2/100) je laisse celà comme ça ou il faut simplifié?

[Luc]

Oui, la c'est p(n) = p(0) + n*a, mais

que vaut p(0) ? (donné dans l'énoncé, c'est la population d'age scolarisé en 2000).
que vaut a? (donné dans l'énoncé, c'est l'augmentation de cette population en un an).

Bon courage,

Luc

Excuse moi, je me suis trompé entre population d'age scolarisé et population effectivement scolarisée.

La formule donnant p(n) n'est pas p(n) = p(0) + n*a. C'est celle donnant s(n). On a donc s(n) = s(0) + n*a.

où s(0) est la population effectivement scolarisée en 2000
et a l'augmentation annuelle de cette population

Pour p(n), c'est un peu plus compliqué, mais pas beaucoup.
On a p(n) = p(0) * (q)^n

où p(0) est la population d'âge scolaire en 2000
et q le taux d'augmentation de cette population en un an. Si tu préfères, c'est le rapport ou

Luc

[emilie78]

si j'ai bien compri s(n) = 70000+(n*2/100)

et p(n)= 70000*150000

[Luc]

si j'ai bien compri s(n) = 70000+(n*2/100)

Non, ce n'est pas 2/100 mais 150 000 (augmentation annuelle de la population scolarisée)
et c'est 700 000 au lieu de 70 000 (mais c'est une faute de frappe je suppose)

et p(n)= 70000*150000

Non, comme je l'ai écrit p(n) = p(0) * q^n.

Où p(0) est la population d'âge 6-11 ans en l'an 2000.
et q le taux d'augmentation annuel de la population 6-11 ans. (En une année, la population 6-11 ans est multipliée par q).

[emilie78]

si j'ai bien compri maintenant

s(n)= s(o)+ (n*a)
=700000+(150000*n)


p(n)= p(o)*q^n
=3000000*(2/100)^n

[Luc]

si j'ai bien compri maintenant

s(n)= s(o)+ (n*a)
=700000+(150000*n)


p(n)= p(o)*q^n
=3000000*(2/100)^n

C'est presque ça!
s(n) est juste

Pour p(n), q = 1 + 2/100 et pas 2/100.
Si tu préfères, p(n+1) = p(n) +2/100 p(n) (L'augmentation de la population p en un an, de l'année 2000+n à l'année 2000+n+1, est 2/100 de la population p à l'année 2000+n).

Luc

[emilie78]

c) par contre pour le c) je sais pas comment on fait pour montrer que c'est une suite arithmétique

j'ai fais le d) et je trouve p(n)= p(o)* q a la puissance p
=700000*150000^5

[Luc]

Tu t'embrouilles entre p et s, suite géométrique et arithmétique

Reprenons au 2)b): exprime le terme p indice n+1 en fonction de p indice n. en déduire l'expression de p indice n.

cf post de Mathusalem

Tu as P_0 tu sais que p_1 = 2% de plus que l'annee precedente.
Donc, en general, si a une certaine annee, tu as une population p_n, combien auras tu de population l'annee suivante ?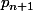 ? 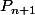= Un certain facteur * p_n.
Je te laisse trouver ce facteur bien precis, a savoir qu'il doit symboliser une croissance de 2%. En trouvant ce facteur, et sachant la valeur de P_0 tu devrais trouver l'expression general de P_n pour ce probleme.

2)c) Meme procede, sauf qu'il faut te rendre compte que ce n'est pas comme pour P_n. Mais c'est une Addition d'enfants par annee.
Par consequent S_n+1 = Un certain nombre a + S_n
Donc S_n = n* a + S_0 (Et ça, c'est la définition d'une suite arithmétique).

2)d) Il faut calculer S_5/P_5, en remplaçant n par 5 dans les formules.

S_5= S_0 + 5*(un certain nombre a)
P_5 = P_0 * (un certain facteur q)^5

Luc

[emilie78]

j'ai rien du tt compris au b) enfaite

[Luc]

Tu sembles avoir du mal à comprendre le concept de suite géométrique. Ce n'est pas grave, mais tu dois le comprendre si tu veux résoudre ton exercice. Voila un exemple "concret" pour te faire saisir ce qu'est une suite géométrique.

Un jeune homme se préparait à l' examen du baccalauréat; son père, pour l' encourager, lui demanda ce qu' il désirait en récompense. Mon examen devant avoir lieu le 20 juin, répond-t-il, donne moi seulement 1 centime le 1er juin, 2 centimes le lendemain, 4 centimes le surlendemain, en doublant chaque jour jusqu'au 20 inclusivement. J' emploierai cet argent à faire un voyage pendant les vacances.

Le père pensa qu' avec cette somme son fils n' irait pas loin; mais au bout de quelques jours, il commença à s' apercevoir de son erreur.

Pourquoi?

Une autre histoire bien connue:

Le jeu d' échec fut inventé par un mathématicien indien. le Roi à qui il le communiqua en fut si émerveillé qu' il dit à l' inventeur de choisir lui-même la récompense qu' il désirait. Or l' échiquier se compose de 64 case.

Le mathématiciens demanda 1 grain de blé pour la première case, 2 grains pour la deuxième, 4 grains pour le troisième et ainsi de suite en doublant toujours le nombre de grains d' une case à la suivante jusqu 'à la dernière.

Tout le monde fut étonné de la modicité d' une pareille demande; mais on fut bien plus surpris quand le mathématicien, ayant fait son calcul, prouva au roi que son royaume ne suffirait pas à produire en plusieurs années tout le blé qu' il demanderait.

Luc

[emilie78]

parce ue ça se multiplie à chaque fois le lendemain par la sommes qu'il avait la veille,

[Luc]

parce ue ça se multiplie à chaque fois le lendemain par la sommes qu'il avait la veille,

Pas tout à fait: 1 le jour 1, 2 le jour 2, 4 le jour 3, 8 le jour 4, etc.

Si le père a donné x un certain jour, que donne-t-il le lendemain?

Luc

[emilie78]

ce serait x^(x+1)?

[Luc]

Non, c'est 2x.

Chaque jour, on multiplie par 2 la somme versée.
On dit que la somme versée , en centimes, est une suite géométrique de raison 2 (et de premier terme 1)

Et pour les grains de blé sur l'échiquier?

Luc

[emilie78]

Merciii beaucoups de ton aide, mais jcrois que jvais arrété mon exercice là,je comprend vraiment rienn, en bonne littéraire que je suis, les maths sont du chinois pour moiii...