Problème avec les identiter remarquable du troisieme degrés!

[missceline]

Bonjour j'ai un gros problème avec un exercice sur les identiter remarquable du troisieme degré!! :hein:

on me demande tout d'abord de la démontrer :
(a+b)^3= a^3 +3 a^2 b + 3 a b^2 + b^3?je ne vois pas comment de montrer :doh: cette identiter remarquable je m'y connait qu'au second degré!
on me demande ensuite de calculer "a la mains"
10.001^3

et enfin on me demande de quel ordre est l'erreur comise par la calculatrice pour ce meme calcul!

Je ne comprend vraiment pas j'avait jamais vue d'identiter remarquable de ce type!!? pourrait on m'expliquer la demarche a effectuer pour cette exo jsuis perdu depuis des heures!?
Merci d'avance :we:

[phryte]

Bonsoir.

10.001^3

tu fais 10001 = 10000 + 1
...

[missceline]

j'ai pas bien compris pourquoi on aditionne 10 000 et 1 parcque on me demande de demontrer l'identiter remarquable!!

[Rower]

Alors pour expliquer
10001 = 10000 + 1
donc

10001^3= (10000+1)^3

Ainsi dans ta formule ton a=10000 et ton b=1

[Timothé Lefebvre]

Salut, pour l'ordre d'erreur de la calculatrice, il suffit de voir qu'elle te donne une valeur approchée d'environ

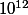
[missceline]

Alors pour expliquer
10001 = 10000 + 1
donc

10001^3= (10000+1)^3

Ainsi dans ta formule ton a=10000 et ton b=1

mon problème c que ce n'est pas 10 001^3 mais 10.001^3 il y a une virgule c'est dix virgule zero zero un!

sinon est ce que je peut faire a=10.000 et b=0.001 :hein:

[Timothé Lefebvre]

sinon est ce que je peut faire a=10.000 et b=0.001 :hein:

Exact c'est ça !

Alors mon message ci-dessus n'est pas bon, désolé.
Je ne vois pas d'erreur de la calculatrice possible puisque même à la main

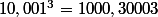
[Clu]

Pour démonter l'identité remarquable, développe toi même le produit :


(a+b)^3=(a+b)²*(a+b)


Il ne te reste plus qu'à finir...

[missceline]

merci pour votre aide elle m'a été utile je n'avait absolument rien compris maintenant c'est plus claire! :we:

[Rower]

Désolé j'ai fait sauté la virgule mais ça revient au meme ^^ la logique est toujours la,

La négligence est l'un de mes moindres défauts :stupid_in

[echevaux]

Bonjour

Exact c'est ça !
Alors mon message ci-dessus n'est pas bon, désolé.
Je ne vois pas d'erreur de la calculatrice possible puisque même à la main

Ce qui est faux :
a 3 décimales donc en a 9 la 9ème étant 1.
et n'en a que 5 les 4 autres avalées par la calculatrice ou ... la main.