Egalité et équivalence ?

[frifrou]

Salut à vous, voilà une petite (mais importante pour moi) question que je me pose :
posons A=[2(x-1)²]/(x-1)
Après simplification on obtiens : A=2x-2

Mais est-ce que A=[2(x-1)²]/(x-1) <=> A=2x-2 ??
Étant donné que le premier est valable sur R\{1} et l'autre sur R tout entier
Merci par avance ! :we:

[fatal_error]

Salut,

c'est pas très propre, mais je pense qu'on peut faire comme ca:


Et

Donc on peut prolonger la premiere relation par continuité en 1 avec et comme sur IR

Fatal_Error, pro des trucs foireux :briques:

[COTLOD]

Dire que est valable sur R\{1} revient à dire :
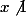
" ET "

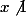
Il n'y a pas de raison que ce "" disparaisse après la simplification de ""

Formellement :
Si "A""B" alors "A ET C""B ET C"

[frifrou]

Merci pour vos réponses à tous les deux,
mais c'est un peu un échappatoire je trouve ta réponse fatal_error,
et en fait il n'ya rien de compliqué lol, ton explication est très claire cotlod.
Merci encore à vous deux! bonne soirée