Intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
TonyPi
- Messages: 3
- Enregistré le: 28 Oct 2008, 11:23
-
par TonyPi » 28 Oct 2008, 20:50
Bonjour à tous,
J'ai un exercice sur les intégrales qui me pose un certain nombre de problèmes...
Soit f(x)=[intégrale entre 0 et pi/2 de..](dt/(1+xsint))
Montrer les égalités suivantes :
f(x)=(arccos x)/(sqrt(1-x²)) pour -1
f(x)=(ln(x+sqrt(x²-1)))/(sqrt(x²-1)) pour x supérieur à 1
Merci de votre aide.
Matheuxx
par busard_des_roseaux » 29 Oct 2008, 02:01
bjr,
pour la (1) , poser:
=\frac{2u}{1+u^2})
soit
)
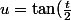l'intégrale devient:
(1)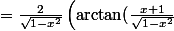 -\arctan(\frac{x}{\sqrt{1-x^2}}) \right))
utiliser ensuite:
-arctan(b)=arctan(\frac{a-b}{1+ab}))
)
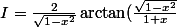}{\sqrt{1-x^2}})
car
=\frac{1-tan^2(z)}{1+\tan^2(z)})
question (3)On obtient la même intégrale
(1) , qui se primitive cette
fois en logarithme et non pas en arctangente, si |x| >1.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 261 invités
