Fonctions !
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
mliiie
- Membre Naturel
- Messages: 34
- Enregistré le: 31 Mar 2008, 23:18
-
 par mliiie » 21 Oct 2008, 18:25
par mliiie » 21 Oct 2008, 18:25
bonjour pourriez vous m'aider :
f(x) = (1-x) * racine(1-x^2) Df : ]-1;1[
et je dois montrer que fx) est dérivable en 1 et préciser f'(1)
Je sais la formule T(h) = f(a-h)-f(a)/h mais je n'arrive à rien ! J'ai vraiment besoin d'aide merci
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 21 Oct 2008, 18:57
par rene38 » 21 Oct 2008, 18:57
Bonsoir
Je sais la formule T(h) = (f(a-h)-f(a))/h
Tu sembles oublier que
- le a de ta formule c'est 1
- le nombre dérivé en a -s'il existe- est la limite de T(h) lorsque h tend vers 0
-
mliiie
- Membre Naturel
- Messages: 34
- Enregistré le: 31 Mar 2008, 23:18
-
 par mliiie » 21 Oct 2008, 19:57
par mliiie » 21 Oct 2008, 19:57
oui je sais tout ca mais je n'y arrive pas quand meme
-
mliiie
- Membre Naturel
- Messages: 34
- Enregistré le: 31 Mar 2008, 23:18
-
 par mliiie » 21 Oct 2008, 20:03
par mliiie » 21 Oct 2008, 20:03
meme que f(1) = 0
-
mliiie
- Membre Naturel
- Messages: 34
- Enregistré le: 31 Mar 2008, 23:18
-
 par mliiie » 21 Oct 2008, 21:38
par mliiie » 21 Oct 2008, 21:38
s'il vous plait
-
Huppasacee
- Membre Complexe
- Messages: 2635
- Enregistré le: 22 Jan 2008, 23:05
-
 par Huppasacee » 21 Oct 2008, 22:00
par Huppasacee » 21 Oct 2008, 22:00
Déjà posté
as tu essayé de voir ce que tu peux faire de ce que je t'ai indiqué ?
f(x) = (1-x) * racine(1-x^2)
1 - x² = (1-x)(1+x)
on a donc
f (x) = (1-x)^3/2 ((1+x)^1/2
et le problème de dérivabilité ne se pose plus lorsqu'on calcule la limite de f '(x) lorsque x tend vers 1)
-
mliiie
- Membre Naturel
- Messages: 34
- Enregistré le: 31 Mar 2008, 23:18
-
 par mliiie » 22 Oct 2008, 19:37
par mliiie » 22 Oct 2008, 19:37
mais j'ai pas compris f(x) = ((1-x)^3)/2 ((1+x)^1)/2 ?
ou alors f(x) = (1-x)^3/2 avec la puissance qui es de 3/2 ?
-
turbeoman
- Membre Naturel
- Messages: 78
- Enregistré le: 08 Oct 2008, 20:55
-
 par turbeoman » 22 Oct 2008, 20:09
par turbeoman » 22 Oct 2008, 20:09
f'(x)=-;)(1-x²)-((1-x)x)/;)(1-x²)
Donc f'(1) impossible car ça fait à chaque fois ;)0!!
-
Huppasacee
- Membre Complexe
- Messages: 2635
- Enregistré le: 22 Jan 2008, 23:05
-
 par Huppasacee » 22 Oct 2008, 23:00
par Huppasacee » 22 Oct 2008, 23:00
Voilà un éclaircissement :
f(x) = (1-x) * racine(1-x^2)
1 - x² = (1-x)(1+x)

cela fait
f(x) =

= (
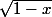
) ^3 *
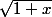
qui peut s'écrire aussi
(1-x) à la puissance 3/2 * racine de (1+x)
= u * v
avec
u = (1-x) ^3/2
et
v =
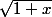
Sais tu dériver cela ?
-
mliiie
- Membre Naturel
- Messages: 34
- Enregistré le: 31 Mar 2008, 23:18
-
 par mliiie » 23 Oct 2008, 17:26
par mliiie » 23 Oct 2008, 17:26
mais ca sert a rien de faire j'ai dmandé a mon prof il m'a dit ki falai faire avec la formule f(a+h)-f(a) / h
-
Huppasacee
- Membre Complexe
- Messages: 2635
- Enregistré le: 22 Jan 2008, 23:05
-
 par Huppasacee » 23 Oct 2008, 17:30
par Huppasacee » 23 Oct 2008, 17:30
Excuse moi alors !!!! ( mille fois suffiront !!)
Où en es tu arrivée , alors dans tes calculs
Peux tu montrer le début et où tu t'es arrêtée ?
-
mliiie
- Membre Naturel
- Messages: 34
- Enregistré le: 31 Mar 2008, 23:18
-
 par mliiie » 23 Oct 2008, 18:02
par mliiie » 23 Oct 2008, 18:02
T(h) = f(1-h)-f(1) / h
= (1-(1+h))(Racine(1-(1+h^2))) / h
=-h(Racine(-2h-h^2)) /h
=(Racine(h^2)(2/h-1))
Ensuite je dois faire la limite mais je ne sais pas si se ke j'ai trouvé est juste
-
mliiie
- Membre Naturel
- Messages: 34
- Enregistré le: 31 Mar 2008, 23:18
-
 par mliiie » 23 Oct 2008, 19:28
par mliiie » 23 Oct 2008, 19:28
si'il te plait huppasacee toi seul peut m'aider !
-
mliiie
- Membre Naturel
- Messages: 34
- Enregistré le: 31 Mar 2008, 23:18
-
 par mliiie » 23 Oct 2008, 19:48
par mliiie » 23 Oct 2008, 19:48
pouvais vous m'aider à calculer T(h) = f(a+h)-f(a)/h
-
Huppasacee
- Membre Complexe
- Messages: 2635
- Enregistré le: 22 Jan 2008, 23:05
-
 par Huppasacee » 23 Oct 2008, 22:26
par Huppasacee » 23 Oct 2008, 22:26
f(x) = (1-x) * racine(1-x^2)
f(1) =0
f(1+h) - f(1) = f(1+h)
remarquons que h doit être négatif=
) \sqrt{1-(1+h)² })
= -h racine (-h² -2h)
Si on divise par h
il reste
- racine (-h²-2h)
et quand h tend vers 0
la racine tend vers 0 ( racine de 0 )
donc la limite est 0
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
