Suite

[bfo]

Bonjour.
Il se trouve que je suis bloqué par un truc ridicule :
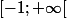
f la fonction définie sur par
1)Variations de f--->j'ai dit croissante.
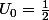
2)Soit la suite telle que : et .
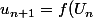Et on me dit de montrer que et j'y arrive sauf pour montrer que c'est inférieur à 1.
Merci de votre aide.
:we:

[valentin.b]

Pour le 1) Tu te contente de dire qu'elle est croissante ? Il faudrait avoir une petite démarche explicative !? Non ?

[Euler911]

Bonjour,

Pour la 2), as-tu déjà vu ce qu'est une démonstration par récurrence???

[valentin.b]

Je cherchais un truc aussi. Je crois que y'a que ça à faire

[Euler911]

1)Variations de f--->j'ai dit croissante.

En effet ça manque de justif' :p

[bfo]

Si je n'ai pas justifié pour les variations de f c'est simplement parce que ça n'est pas là que se situe mon problème.
Autrement, oui, j'ai un peu vu la récurrence mais pas dans le cas d'une inégalité...que pour des égalités si vous voyez ce que je veux dire.

[Euler911]

Essaye alors de suivre la schéma de la récurrences: hypothèses, hérédité,...

Essaye déjà les deux premières étapes et poste ce que tu as trouvé

[bfo]

Désolé mais l'inégalité me gêne beaucoup.

[Euler911]

Bien, P(n)=

P(1) est-elle vraie?

On suppose P(n) vraie donc P(n+1) est vraie.

Que vaut P(n)???

[bfo]

P(1) est vraie.
Donc on peut se lancer, ça ok.
Mais je ne vois pas pourquoi tu poses la question "que vaut P(n)" puisque on le sait, c'est ce qu'on doit prouver, non ?

[Euler911]

2cris ça autrement (avec les radicaux...)

[bfo]

mais pourquoi ?

[Euler911]

Ben c'est comme ça :doh: :hein: lis ton énoncé!

[bfo]

Bien, ça va pour cette question, j'ai enfin réussi.
Mais maintenant, il faut montrer que pour tout n entier naturel, et la seule chose qui me gêne, ce sont les valeurs absolues.
Alors est-ce que les omettre, et voir la récurrence pour les carrés des deux membres est équivalent ?