R est-il un plan ?
21 messages
- Page 1 sur 2 - 1, 2
R est-il un plan ?
Bonjour,
tout est dans le titre si je puis dire. Je me suis posé cette question il y a quelques années, j'ai cherché un peu, je n'ai jamais pu y répondre.
De façon plus détaillée : On sait par exemple que l'ensemble des nombres
complexes est un R-plan, c'est à dire un espace vectoriel de dimension 2 sur
le corps des réels. Alors je me demande s'il existe un corps K tel que R soit
un K-plan ! (R désigne l'ensemble des nombres réels).
Je sais que si K existe alors il contient Q (l'ensemble des rationnels).
Peut-être pourriez-vous m'indiquer des idées pour répondre à cette question. Je me demande aussi à quel domaine des maths cette question fait appel.
Merci pour votre aide
tout est dans le titre si je puis dire. Je me suis posé cette question il y a quelques années, j'ai cherché un peu, je n'ai jamais pu y répondre.
De façon plus détaillée : On sait par exemple que l'ensemble des nombres
complexes est un R-plan, c'est à dire un espace vectoriel de dimension 2 sur
le corps des réels. Alors je me demande s'il existe un corps K tel que R soit
un K-plan ! (R désigne l'ensemble des nombres réels).
Je sais que si K existe alors il contient Q (l'ensemble des rationnels).
Peut-être pourriez-vous m'indiquer des idées pour répondre à cette question. Je me demande aussi à quel domaine des maths cette question fait appel.
Merci pour votre aide
Euh...  est de dimension 1 donc je dirais que c'est plutôt une droite...
est de dimension 1 donc je dirais que c'est plutôt une droite...
Si tu prends un point appartenant à , tu vois qu'il n'a qu'une coordonnée, je vois mal comment
, tu vois qu'il n'a qu'une coordonnée, je vois mal comment  pourrait définir un plan ~~
pourrait définir un plan ~~
 peut être représenté graphiquement par
peut être représenté graphiquement par  , là c'est un plan : un point appartenant à
, là c'est un plan : un point appartenant à  a deux coordonnées : sa partie réelle et sa partie imaginaire.
a deux coordonnées : sa partie réelle et sa partie imaginaire.
Après, il faut savoir ce que l'on entend par droite, plan... il faut plutôt raisonner en terme de dimension d'espace vectoriel.
Je crois que ta question fait appelle à des notions de topologie, mais je n'ai fait qu'aborder cette partie compliquée des mathématiques en SPE, donc s'il y a des connaisseurs, je les laisse te répondre ^^
Si tu prends un point appartenant à
Après, il faut savoir ce que l'on entend par droite, plan... il faut plutôt raisonner en terme de dimension d'espace vectoriel.
Je crois que ta question fait appelle à des notions de topologie, mais je n'ai fait qu'aborder cette partie compliquée des mathématiques en SPE, donc s'il y a des connaisseurs, je les laisse te répondre ^^
Bonjour,
Si est un sous-corps de
est un sous-corps de  tel que
tel que  est un
est un  -espace vectoriel de dimension finie, alors
-espace vectoriel de dimension finie, alors  est un sous-
est un sous- -espace vectoriel fermé de
-espace vectoriel fermé de  : on choisit une
: on choisit une  -base de
-base de  adaptée à
adaptée à ) , et comme la convergence dans
, et comme la convergence dans  (=
(= 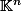 ) est équivalente à la convergence coordonnée par coordonnée, la limite d'une suite convergente d'éléments de
) est équivalente à la convergence coordonnée par coordonnée, la limite d'une suite convergente d'éléments de  est dans
est dans  .
.
 est le complété de
est le complété de  pour la norme « valeur absolue », et
pour la norme « valeur absolue », et  est un sous-espace fermé de
est un sous-espace fermé de  donc il est aussi complet, d'où
donc il est aussi complet, d'où  inclus dans
inclus dans  . Comme
. Comme  inclus dans
inclus dans  on a
on a  et n = 1.
et n = 1.
Si
Shaolan a écrit:Euh...est de dimension 1 donc je dirais que c'est plutôt une droite...
Si tu prends un point appartenant à, tu vois qu'il n'a qu'une coordonnée, je vois mal comment
pourrait définir un plan ~~
Là, ça commence à m'intéresser =P
Je me doute que c'est un peu plus complexe que ça, et qu'il faut préciser sur quoi l'on travaille, avant de se poser cette question.
Si je relis ta démonstration, tu as donc prouvé que est de dimension 1 sur n'importe lequel de ses sous-corps, c'est bien cela ?
est de dimension 1 sur n'importe lequel de ses sous-corps, c'est bien cela ?
Alors j'ai une question pour terminer, est-ce qu'il y a équivalence entre espace-vectoriel de dimension 1 et droite ? ou faut-il préciser qu'il s'agit d'une droite vectorielle ?
PS : vu les termes de "normes" ou "espace complet" que tu utilises, cette question fait bel et bien appelle à des notions de topologie ^^
Je me doute que c'est un peu plus complexe que ça, et qu'il faut préciser sur quoi l'on travaille, avant de se poser cette question.
Si je relis ta démonstration, tu as donc prouvé que
Alors j'ai une question pour terminer, est-ce qu'il y a équivalence entre espace-vectoriel de dimension 1 et droite ? ou faut-il préciser qu'il s'agit d'une droite vectorielle ?
PS : vu les termes de "normes" ou "espace complet" que tu utilises, cette question fait bel et bien appelle à des notions de topologie ^^
Shaolan a écrit:Si je relis ta démonstration, tu as donc prouvé queest de dimension 1 sur n'importe lequel de ses sous-corps, c'est bien cela ?
Non, il est de dimension infinie sur n'importe lequel de ses sous-corps stricts, et de dimension 1 sur lui-même.
Un espace vectoriel de dimension 1 sur un corps K est égal (ou isomorphe) à K.
Alors j'ai une question pour terminer, est-ce qu'il y a équivalence entre espace-vectoriel de dimension 1 et droite ? ou faut-il préciser qu'il s'agit d'une droite vectorielle ?
Oui mais quand on parle de dimension c'est toujours sur un corps donné : C est de dimension 2 sur R mais de dimension 1 sur C par exemple. Si on considère que le corps de base est R, C est un plan; si on considère que c'est C, C est une droite. On peut préciser « R-plan » ou « C-droite » pour que ce soit clair. Dans le monde réel quand on parle de dimension 1 ou 2 ou 3 ou plus, c'est sur R, mais en maths on n'est pas dans le monde réel
« Droite vectorielle » sert à faire la distinction avec les droites affines, qui ne sont pas forcément des sous-espaces vectoriels.
Voilà !!
Merci beaucoup, c'est bien plus clair dans ma tête maintenant ^^
Sauf le "de dimension infinie"... mais j'ai toujours eu du mal avec la dimension infinie ^^'
En résumé :
R est de dimension infini sur tous ses sous-corps stricts
R est de dimension 1 sur lui-même
R est de dimension 1 sur tout corps dont il est un sous-corps
Et je suppose que ça n'a pas de sens de parler de dimension de R sur un corps dont il n'est pas un sous-corps ?
Donc R ne peut pas être considéré comme un plan.
Merci beaucoup, c'est bien plus clair dans ma tête maintenant ^^
Sauf le "de dimension infinie"... mais j'ai toujours eu du mal avec la dimension infinie ^^'
En résumé :
R est de dimension infini sur tous ses sous-corps stricts
R est de dimension 1 sur lui-même
R est de dimension 1 sur tout corps dont il est un sous-corps
Et je suppose que ça n'a pas de sens de parler de dimension de R sur un corps dont il n'est pas un sous-corps ?
Donc R ne peut pas être considéré comme un plan.
Shaolan a écrit:R est de dimension 1 sur tout corps dont il est un sous-corps
Àh ben non, pour parler de dimension de R sur un corps K, il faut que le corps K soit « plus petit » que R (il faut que R soit un K-espace vectoriel). On ne peut pas parler de dimension de Q sur R car Q n'est pas un R-espace vectoriel.
Et je suppose que ça n'a pas de sens de parler de dimension de R sur un corps dont il n'est pas un sous-corps ?
Dont il n'est pas un surcorps.
abcd22 a écrit:Siest un sous-corps de
tel que
est un
-espace vectoriel de dimension finie, alors
est un sous-
-espace vectoriel fermé de
: on choisit une
-base de
adaptée à
, et comme la convergence dans
(=
) est équivalente à la convergence coordonnée par coordonnée, la limite d'une suite convergente d'éléments de
est dans
.
est le complété de
pour la norme « valeur absolue », et
est un sous-espace fermé de
donc il est aussi complet, d'où
inclus dans
. Comme
inclus dans
on a
et n = 1.
Shaolan a écrit:Et qu'est-ce qu'un surcorps alors ? je ne l'ai pas trouvé dans wikipedia...
Un surcorps de R est un corps qui contient R. On dit aussi « extension de corps ».
Donc C est de dimension 2 sur R et R n'a pas de dimension sur C, puisque C est "plus grand" que R (ou puisque R est "plus petit" que C, ça revient au même). C'est bien ça ?
Oui.
Super ! Je ne pensais vraiment pas que la réponse était aussi courte. Juste pour info, as-tu créé cette démo ou l'as tu vu quelque part ? Quel est ton niveau ? (juste par curiosité)
Merci beaucoup en tout cas, cette réponse me touche ! les vielles questions qui vous taraudent pendant des heures ! C'est beau la topo. C'est toujours agréable de voir la réactivité des gens sur le forum :we:
Merci beaucoup en tout cas, cette réponse me touche ! les vielles questions qui vous taraudent pendant des heures ! C'est beau la topo. C'est toujours agréable de voir la réactivité des gens sur le forum :we:
Shaolan a écrit:Ben c'est clair qu'on n'a pas vu grand chose en topo en prépa...
Contrairement à certains, j'ai bien aimé ce chapitre, voire plus que les autres.
Je me demande si on utilise de la topo dans des maths appiquées... j'aimerais bien voir ça ^^
Je suis aussi curieux de connaitre le niveau de abcd22 =D
Moi je fais des systèmes dynamiques en particulier. Donc souvent ça fait appel à de la topo (fermé, convexe, compact...) pour des notions de stabilité de systèmes en particulier. C'est un domaine très intéressant (je trouve, ok c'est pas très objectif) avec des applications dans le domaine du vivant assez surprenantes par exemple.
abcd22 a écrit:est un sous-
-espace vectoriel fermé de
: on choisit une
-base de
adaptée à
, et comme la convergence dans
(=
) est équivalente à la convergence coordonnée par coordonnée, la limite d'une suite convergente d'éléments de
est dans
.
Après réflexion, ça ne marche pas, car ça suppose que K est complet au départ donc on tourne en rond... et je ne vois pas de moyen simple de contourner le problème. D'après une recherche rapide sur internet le résultat est quand même vrai mais la démonstration utilise plutôt de la théorie de Galois, il y notamment une discussion sur les-mathematiques.net à ce sujet, que je n'ai pas lue en détail.
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
