Continuité de fractions rationnelles à deux variables

[nyth]

Bonjour, j'ai besoin d'aide pour ces fonctions là:

1)f:R² -> R


Voici mon raisonnement:
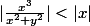
et comme alors donc continue en (0,0).
est-ce que ce raisonnement est correct ?

2) la dérivée partielle en x:
Je dois chercher en quels points de R² la dérivée est continue. En R²\(0,0) c'est trivial, mais en (0,0) je trouve pas de majoration ou de minoration qui me permettent de conclure (en passant à la limite):/

3) pareil en y:

Merci d'avance de votre aide

[Maxmau]

Bj

1/ OK

2/ Sans doute n'y-a-t-il pas continiuité en (0,0)

[nyth]

Pour prouver que la dérivée partielle en x n'est pas continue en 0, il faudrait donc la minorer par une fonction qui ne tend pas vers 0 en (0,0) ? ou y at-il une autre méthode ?

Si c'est bien ça, je sèche, je ne trouve pas de minoration qui me permettent de conclure...
J'ai deux minoration potentielles:



et



après je vois pas comment faire :/
En tout cas merci de ton aide Maxmau

[Antho07]

On peut aussi passer en polaire et faire tendre r vers 0.
Si la limite depend de theta alors il n'y pas continuité.

[Maxmau]

Ou alors faire tendre (x,y) vers (0,0) , le point (x,y) restant
sur la droite y = mx

[nyth]

Ah mais bien sûr !

sur la droite (x,x) on a

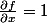
Donc ne tend pas vers 0

merci, j'aurai dû y penser plus tôt >_<