Les suites

[blade_ounet]

Bonjour,

Soit la suite U définie par U0=2 ; U1=2 et la relation de récurrence R:8un+2=6un+1-Un pour tout entier naturel n.

1.Calculer U2 ; U3 .

2.Déterminer les suites géométriques vérifiant la relation R.

3.Montrer que si deux suites V et W de termes Vn et Wn vérifient la relation R,alors la suite T dont les termes sont définies par Tn=Vn+Wn vérifie la relaion R.

4.Déduire de ce qui précède l'expression de Un en fonction de n.

Pourriez vous m'aider svp c'est mon derniere exercice le seul que ji arrive pas. Merci

[Benjamin]

Salut,
Pour calculer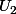 et 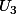, c'est pas très dur, il suffit d'utiliser puisque tu connais U0 et U1.
Pour la suite, il faut résonner de manière générale. Une suite géométrique est définie par le fait qu'il existe un réel q (la raison) tel que . Tu peux donc calculer et 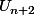en fonction de et q et voir quelle condition cela impose sur q pour respecter la relation (R). Tu dois normalement trouver 3 raisons géométriques q différentes vérifiant (R).

[blade_ounet]

Ok merci j'ai trouver pour U2 et U3 met apres sa reste quand meme confus

[blade_ounet]

Bon je vais en cours si quelq'un pourrait m'aider pendant mon absence ou a mon retour sa serai sympa merci a se soir !

[Benjamin]

Tu poses une suite Un géométrique qui vérifie R : Soit Un une suite géométrique vérifiant R. Alors, il existe U0 et q dans R tel que .

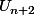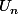Puis tu écris le fait que vérifie (R), en remplaçant , et en fonction de et q.
Puis tu déroules ton équation jusqu'à arriver aux 3 solutions de q.

Ensuite, il ne faut pas oublier la réciproque. Tu prends les 3 suites géométriques trouvées et tu vérifie qu'elles vérifient (R).