bonsoir, j'ai de nouveau un probléme sur une integrale:
j'esseye de mq:
int(0 a 1,(x^k)f(x)dx)=1/(exp(2*i*Pi*k)-1)*int(|z|=1,(z^k)f(z)ln(z)dz).
hypothese sur k: k rèels, k>-1, k nappartient pas a N.On nous propose d'utiliser la determination de la puissance associè au logarithme definit sur C-R+, d'argument a valeur dans ]0,2pi[
Probleme intégrale.
6 messages
- Page 1 sur 1
phillipe20 a écrit:bonsoir, j'ai de nouveau un probléme sur une integrale:
j'esseye de mq:
int(0 a 1,(x^k)f(x)dx)=1/(exp(2*i*Pi*k)-1)*int(|z|=1,(z^k)f(z)ln(z)dz).
hypothese sur k: k rèels, k>-1, k nappartient pas a N.On nous propose d'utiliser la determination de la puissance associè au logarithme definit sur C-R+, d'argument a valeur dans ]0,2pi[
Il y a bien ln(z) dans la dernière intégrale ?
Bonjour Phillipe20,
comme Maxmau te l'a déjà fait remarquer, on a le même problème que dans ton autre post l'intégrale d'une fonction complexe sur un chemin n'est définie que pour les fonctions continues sur ce chemin ce qui n'est pas le cas de la fonction\ln(z)) sur {z; |z|=1}.
sur {z; |z|=1}.
Ce qui m'amène à te poser ces questions : d'où sort cet exercice ? Y avait-il d'autre questions avant qui justifieraient la notation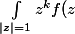\ln(z)dz) (genre prolongement par continuité au cas où f(1)=0 ) ?
(genre prolongement par continuité au cas où f(1)=0 ) ?
Ce qui m'embête c'est que je me rappelle avoir déjà vu ce genre d'exercice il y a longtemps mais je ne me souviens plus où...
comme Maxmau te l'a déjà fait remarquer, on a le même problème que dans ton autre post l'intégrale d'une fonction complexe sur un chemin n'est définie que pour les fonctions continues sur ce chemin ce qui n'est pas le cas de la fonction
Ce qui m'amène à te poser ces questions : d'où sort cet exercice ? Y avait-il d'autre questions avant qui justifieraient la notation
Ce qui m'embête c'est que je me rappelle avoir déjà vu ce genre d'exercice il y a longtemps mais je ne me souviens plus où...
tize a écrit:Bonjour Phillipe20,
comme Maxmau te l'a déjà fait remarquer, on a le même problème que dans ton autre post l'intégrale d'une fonction complexe sur un chemin n'est définie que pour les fonctions continues sur ce chemin ce qui n'est pas le cas de la fonctionsur {z; |z|=1}.
Ce qui m'amène à te poser ces questions : d'où sort cet exercice ? Y avait-il d'autre questions avant qui justifieraient la notation(genre prolongement par continuité au cas où f(1)=0 ) ?
Ce qui m'embête c'est que je me rappelle avoir déjà vu cela il y a longtemps mais je ne me souviens pas où...
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
