Convergence cosinus

[PANAMIEN]

Soient (Un) et (Vn) deux suites.
Un = cos(pis/2^2) cos(pis/2^3)... cos(pis/2^n)
et Vn = Un sin(pis/2^n)

1-Montrer que la suites (Un) converge
2-Montrer que la suite (Vn) est une suite geometrique. En deduire la limite de (Un)

J'ai montré que U(n+1)/Un<1
Donc Un decroissante.
pis/2^n < pis/4
donc cos(pis/2^n) > cos(pis/4)
Donc Un converge.

Est ce que c'est bon ? J'en suis pas convaincu.

Ensuite j'ai trouvé Vn=(1/2)^(n-1) mais je n'arrive pas a le demontrer.

J'ai besion d'un coup de main svp.

[LN1]

Bonjour,

que () soit décroissante est une bonne chose
que est certes vrai pour n > 2 mais n'apporte rien à l'affaire

En revanche tu peux prouver que > 0 et utiliser le théorème des suite décroissantes minorées

Pour la nature de ()
Calcule , d'abord en fonction de
puis, sachant que trouve en fonction de
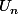
Enfin, en utilisant le fait que cos(a)sin(a) = (1/2) sin(2a), exprime en fonction de . Tu auras alors prouvé que est géométrique, tu pourras calculer puis en fonction de n

il te restera à calculer la limite (rappel : )

Bon courage

[PANAMIEN]

Pour montrer que Un>0 :
pis/2>pis/2^n>0
donc cos(pis/2^n)>cos(pis/2)=0

Est ce que c est bon ?

[LN1]

tout-à-fait