Problème de maths !
18 messages
- Page 1 sur 1
Problème de maths !
Je dois étudier le signe de (2cos^3x-3cos^2x+1)/(cos^2x) sur 0;(Pi/2)
Et j'avou que c'est assez complexe et que j'ai un peut perdu le sens des maths...
Et j'avou que c'est assez complexe et que j'ai un peut perdu le sens des maths...
J'ai reussit à la rendre plus compréhensible grace à Word et après j'ai fait une capture d'écran...
Vous pouvez voir l'équation à cette URL (copier-coller dans l'explorateur)
http://img107.imageshack.us/img107/214/coco5oe.png
Merci de votre aide future
Vous pouvez voir l'équation à cette URL (copier-coller dans l'explorateur)
http://img107.imageshack.us/img107/214/coco5oe.png
Merci de votre aide future
Bonjour
(rem : Bonjour, pour voir mon code Latex, il suffit que tu cites mon message)
une des première chose à faire est de factoriser au maximum ton expression. Pour ne pas être gêné par les cos, on va poser X = cosx
alors
 s'annule pour X = 1, donc tu peux mettre X - 1 en facteur
s'annule pour X = 1, donc tu peux mettre X - 1 en facteur
factorise ....
tu dois obtenir comme résultat final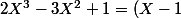(X - 1)(2X + 1))
donc
(\cos x - 1 )(2\cos x +1 )}{\cos^2x})
le signe de chacun de ces facteurs est facile à déterminer sur
(rem : Bonjour, pour voir mon code Latex, il suffit que tu cites mon message)
une des première chose à faire est de factoriser au maximum ton expression. Pour ne pas être gêné par les cos, on va poser X = cosx
alors
factorise ....
tu dois obtenir comme résultat final
donc
le signe de chacun de ces facteurs est facile à déterminer sur
dm pour demain
je dois resoudre un probleme et je n'est pas fait ça depuis longtemps
j'ai dû mal a m'en sortir
une secretaire d'un college a acheté 22 timbres les uns a 2,50 f et les autres
a 2,20 f. Elle a payé en tout 52,9.
combien de timbres de chaque sorte a t-elle achetés?
j'ai dû mal a m'en sortir
une secretaire d'un college a acheté 22 timbres les uns a 2,50 f et les autres
a 2,20 f. Elle a payé en tout 52,9.
combien de timbres de chaque sorte a t-elle achetés?
LNI j'ai aussi posté mon problème dans un autre forum et une autre personne m'a donné une autre solution que la tienne...Les deux entrent en conflit et je n'arrive pas à voir ou est l'erreur !
Voici le lien si tu veux y jeter un coup d'oeil.
http://www.forum.math.ulg.ac.be/viewthread.html?SESSID=8d7656b430b5bd5c50231145785acb77&id=20867
Merci....
Lui (ecrit en LATEX je crois ) écrit la factorisation d'une facon différente mais j'ai l'impression qu'il a fait une erreur de signe!
) écrit la factorisation d'une facon différente mais j'ai l'impression qu'il a fait une erreur de signe!
Voici le lien si tu veux y jeter un coup d'oeil.
http://www.forum.math.ulg.ac.be/viewthread.html?SESSID=8d7656b430b5bd5c50231145785acb77&id=20867
Merci....
Lui (ecrit en LATEX je crois
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 83 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
