Matrice symétrique particulière
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
gontrand
- Messages: 9
- Enregistré le: 23 Fév 2008, 16:03
-
 par gontrand » 23 Fév 2008, 16:16
par gontrand » 23 Fév 2008, 16:16
Bonjour à tous,
voilà je dois en fait résoudre le problème suivant:
On considère une matrice carrée A de dimension n, telle toutes les entrées sur la diagonale sont égales à un complexe u, tandis que toutes les autres entrées sont égales à un complexe v.
On demande:
a) de donner les valeurs propres de A, au moyen de calculs très simples, sans effectuer de calcul de déterminant;
b)soient lambda_1...lambda_p, les p valeurs propres distinctes de A. Montrer que le produit des (A-lambda_i*I) = 0;
c)A est-elle diagonalisable?
Voilà, je vois pas très bien comment faire, donc merci d'avance pour votre aide.
-
Taupin
- Membre Relatif
- Messages: 449
- Enregistré le: 27 Jan 2008, 11:22
-
 par Taupin » 23 Fév 2008, 16:17
par Taupin » 23 Fév 2008, 16:17
Déjà trouve les valeurs propres ;) :zen:
-
gontrand
- Messages: 9
- Enregistré le: 23 Fév 2008, 16:03
-
 par gontrand » 23 Fév 2008, 16:36
par gontrand » 23 Fév 2008, 16:36
En fait, je pense que l'élément de la diagonale est la seule valeur propre, mais je sais pas le montrer rigoureusement.
De plus, ça a pas l'air très cohérent avec le point b...
-
Taupin
- Membre Relatif
- Messages: 449
- Enregistré le: 27 Jan 2008, 11:22
-
 par Taupin » 23 Fév 2008, 16:40
par Taupin » 23 Fév 2008, 16:40
Hum essaye (u-v) comme valeur propre ;) donne moi la dimension et tu comprendras tout de suite je crois ;)
-
gontrand
- Messages: 9
- Enregistré le: 23 Fév 2008, 16:03
-
 par gontrand » 23 Fév 2008, 16:45
par gontrand » 23 Fév 2008, 16:45
Heu oui, j'ai écrit n'importe quoi au-dessus...
Sinon la dimension c'est n en général.
En fait, je crois que a-b est valeur propre de multiplicité n-1, et que la nième valeur propre c'est a+(n-1)*b.
Mais je l'ai trouvé numériquement donc j'ai pas de preuve...
-
Taupin
- Membre Relatif
- Messages: 449
- Enregistré le: 27 Jan 2008, 11:22
-
 par Taupin » 23 Fév 2008, 17:03
par Taupin » 23 Fév 2008, 17:03
Hum tu dis que la matrice A-(u-v)In est de rang 1 donc (u-v) est valeur propre (n-1)ème et tu conclus avec la trace pour trouver la deuxième (et dernière) valeur propre ;)
-
gontrand
- Messages: 9
- Enregistré le: 23 Fév 2008, 16:03
-
 par gontrand » 23 Fév 2008, 17:19
par gontrand » 23 Fév 2008, 17:19
Ok, merci beaucoup.
Une idée pour la diagonalisation ou pas (sans vouloir abuser ;)?
Je pense que ce n'est pas diagonalisable parce que une valeur propre peut être nulle mais je ne sais pas si ça suffit comme argument...
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 23 Fév 2008, 17:38
par kazeriahm » 23 Fév 2008, 17:38
et alors une matrice peut etre diagonalisable et avoir une (plusieurs) valeur(s) propre(s) nulle(s), par exemple la matrice nulle
relis l'énoncé de la question b : que peux-tu dire du polynome
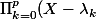})
?
(c'est quoi le Pi du produit en latex ??)
-
Taupin
- Membre Relatif
- Messages: 449
- Enregistré le: 27 Jan 2008, 11:22
-
 par Taupin » 23 Fév 2008, 17:39
par Taupin » 23 Fév 2008, 17:39
Hum je dirais que c'est diagonalisable moi, cherche un vecteur propre associé à la deuxième vp ;)
-
gontrand
- Messages: 9
- Enregistré le: 23 Fév 2008, 16:03
-
 par gontrand » 23 Fév 2008, 18:08
par gontrand » 23 Fév 2008, 18:08
Heu là, franchement, je vois pas très bien...

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 23 Fév 2008, 18:30
par fatal_error » 23 Fév 2008, 18:30
(pour le produit en latex, c'est \prod :
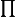
)
la vie est une fête

-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 23 Fév 2008, 19:33
par kazeriahm » 23 Fév 2008, 19:33
le polynome dont je te parlais est scindé et à racines simples sur R (les lambda_k sont distincts) et annule ta matrice. Ca te donne pas une idée ?
-
gontrand
- Messages: 9
- Enregistré le: 23 Fév 2008, 16:03
-
 par gontrand » 24 Fév 2008, 09:04
par gontrand » 24 Fév 2008, 09:04
Heu non, je vois pas ce que ça veut dire un polynome qui annule une matrice, ce serait cool que tu m'expliques pq je suis un peu bloqué ;)
Sinon j'ai encore une question :)
Je dois montrer que pour tout k, A^k= alpha_k*A + beta_k*I,
j'ai commencé par essayer de traiter le cas hors diagonale, pour simplement corriger le terme diagonal avec beta_k*I, mais je ne vois pas de relation...
Si quelqu'un a une idée...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
