Determinant d'une matrice 3x3 particuliere

[uargh]

Bonjour à tous, je cherche désespérément un "truc" pour résoudre le problème suivant :

Soit A =
a b c
a' b' c'
a" b" c"

Avec det(A 1,1)=det (A 1,3) et det(A 3,1)=det(A 3,3)

Il me faut montrer que si b' différent de 0, alors det(A)=0 et que si b'=0 alors det(A) n'est pas forcément nul.

J'ai réussi a trouver ceci : ab"c'=a'bc", et en procédant de même je pense que l'on doit trouver la même chose pour les deux autres "diagonales" de la règle de Sarus. Cependant cela ne m'avance pas.


Aurais-je louper une chose évidente ?

Cordialement. Uargh.

[Nightmare]

Salut !

Je ne comprends pas, que sont tes lettres? A priori ta matrice est quelconque !

[uargh]

Oui elle est quelconque en dehors du fait que les det des sous matrices 2x2 en haut à gauche et en haut a droite sont égales, ainsi que le det des matrices 2x2 en bas a gauche et en bas a droite.

[wserdx]

J'ai un "truc", mais il n'est pas très évident.
Tu trouveras ici une démonstration
comatrice
du fait qu'un mineur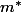 de dimension de la comatrice de et son mineur complémentaire dans la matrice sont liés par la relation

Dans ton cas, on considère un mineur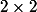 , composés des
4 mineurs de de dimension 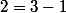, qui sont donc des coefficients de la comatrice de .
Ce mineur est nul puisque tu dis qu'il a deux colonnes égales.
Son mineur complémentaire est .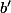
On a donc .