Equation type x²+ay²=z² [arithmétique]
Olympiades mathématiques, énigmes et défis
-
~oa~
- Membre Naturel
- Messages: 40
- Enregistré le: 02 Juil 2007, 18:38
-
 par ~oa~ » 17 Déc 2007, 13:51
par ~oa~ » 17 Déc 2007, 13:51
SALUT
résoudre dans Z^3 l'équation suivante :
x²+5y²=z²
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 17 Déc 2007, 15:47
par lapras » 17 Déc 2007, 15:47
Bonjour,
répndez en blanc svp car je n'ai pas le temps de le faire et jaimerais chercher :=)
Merci :we:
-
fati
- Membre Relatif
- Messages: 427
- Enregistré le: 08 Déc 2007, 23:58
-
 par fati » 17 Déc 2007, 18:19
par fati » 17 Déc 2007, 18:19
non! on te laisse le soin de répondre Lapras!!!
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 17 Déc 2007, 21:15
par ThSQ » 17 Déc 2007, 21:15
Mmm, z²-5y²=x² est une équation de Pell (généralisée). On peut montrer (difficilement) qu'il y a une solution (y0,z0) pour tout x² (développement en fractions continues ...) et que toutes les autres s'obtiennent (facilement) à partir de (y0,z0) et qu'il y en a une infinité.
Je serais surpris (mais super heureux de me tromper !) qu'il y ait une forme explicite de toutes les solutions. :briques:
A noter qu'il n'y a pas d'espoir du côté de

qui n'est pas un anneau fréquentable ....
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 17 Déc 2007, 22:17
par aviateurpilot » 17 Déc 2007, 22:17
ThSQ a écrit:Je serais surpris (mais super heureux de me tromper !) qu'il y ait une forme explicite de toutes les solutions. :briques:
essayons de resoudre l'equation dans

.
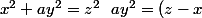(z+x))
soit pour
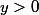
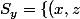\in\mathbb{N}^2|\ (z-x)(z+x)=ay^2\})
il donc evident que
|\ d|ay^2,d\equiv \frac{ay^2}{d}[2] \})
et donc
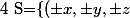|\ (x,y,z)\in\cup_{n\in\mathbb{N}^*}S_n\}\cup \{(\pm x,0,\pm x)|x\in\mathbb{N}\})
verification:
alors par exemple pour construire une solution

on prend par exemple

et donc
=\frac{1}{2}(50-10;50+10)=(20,30))

-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 17 Déc 2007, 22:30
par ThSQ » 17 Déc 2007, 22:30
J'appelle pas ça une forme explicite mais tout est question de convention.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 17 Déc 2007, 22:45
par aviateurpilot » 17 Déc 2007, 22:45
ThSQ a écrit:J'appelle pas ça une forme explicite mais tout est question de convention.
on peux appeler ca une maniere qui peux mener a construire tous les solution possible.
si on te demande par exemple de resoudre dans
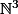
l'equation
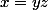
y a t'il une autre solution autre que
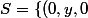,(0,0,z),(x,d,\frac{x}{d})\mathbb{N}|\ d|x,x\in\mathbb{N}^*,(y,z)\in\mathbb{N}^2\})
?
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 18 Déc 2007, 19:25
par Imod » 18 Déc 2007, 19:25
~OA~ très absent depuis le début du fil , sème des graines sur d'autres forums
même sujet , il pourrait aussi apporter son soutien à ceux qui cherchent à l'aider ici :zen:
Imod

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 01 Mar 2008, 00:19
par raito123 » 01 Mar 2008, 00:19
Re tout le monde,
Je pense que j'ai trouver

D:
Je donne direct les soluces :zen: :
 \in \{(k.a_n) ; (kb_n) ; (k) / tel que k \in \mathbb{N}\})
Avec
^n + (9+4sqrt5)^n}2)
^n-a_n}{sqrt5})
.
Ps: en utilisant le binôme de newton on peut montrer que a_n et b_n appartient à

Bonne nuit à tous :happy2:
Si c'est pas juste dites moi pk svp !!!
Les multiples ne doivent pas être utilisés sans nécessité
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités
 qui n'est pas un anneau fréquentable ....
qui n'est pas un anneau fréquentable ....