Theorie de la representation

[Patrick.p]

Bonjour,

j'ai une question d'un probleme concernant la theorie des characteres :

Soit G un groupe fini.
Soit g un element de G.
Soit V une representation (sur les complexes) de G.
X(V)(g) le character pour la representation V evaluer en g.

Montrer que g et g^(-1) sont conjuguer

si et seulement si

X(V)(g) est reel pour tout V.

Si quelqu'un pouvais m'aider. Merci bien

[yos]

Bonjour.
Pour , tu calcules sachant que et tu utilises la symétrie de la trace ().

[busard_des_roseaux]

bonjour,

Si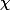 est une fonction multiplicative de G vers

d'où:

d'où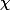 est,en fait, à valeurs dans les nombres complexes de module 1
d'où:


si

donc est réel.


zut,ça ne marche pas avec les matrices de ,
désolé d'avoir pollué le fil... :hum:

[yos]

zut,ça ne marche pas avec les matrices de ,
désolé d'avoir pollué le fil... :hum:

Si c'est ça. Dans le V est en indice : c'est bien une fonction multiplicative définie sur G, à valeurs dans C (donc dans U puisque G est fini).

[busard_des_roseaux]

le V est en indice

ça, d'accord.

le V est en indice : c'est bien une fonction multiplicative définie sur G, à valeurs dans C (donc dans U puisque G est fini).

je ne vois pas si est à valeurs dans ou dans ?

[Patrick.p]

est a valeur dans car il est definie comme la Trace de la matrice associer a g par la representation V de G qui est "a valeur dans ".

Merci pour votre aide.

[yos]

je ne vois pas si est à valeurs dans ou dans ?

C'est V qui est à valeurs dans

[busard_des_roseaux]

merçi bcp.